householder變換

householder變換（Householder transformation），譯為“豪斯霍爾德變換”，或譯“豪斯霍德轉換”，又稱初等反射（Elementary reflection），最初由A.C Aitken在1932年提出。householder變換最初由A.C Aitken在1932年提出。Alston Scott Householder在1958年指出了這一變換在數值線性代數上的意義。這一變換將一個向量變換為由一個超平面反射的鏡像，是一種線性變換。其變換矩陣被稱作豪斯霍爾德矩陣，在一般內積空間中的類比被稱作豪斯霍爾德運算元。超平面的法向量被稱作豪斯霍爾德向量。

基本信息

• 中文名：householder變換
• 英文名：Householder transformation

• 別 稱：豪斯霍爾德變換
• 相關人物：Alston Scott Householder

定義

householder變換

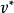householder變換

householder變換

householder變換

如果 給出為單位向量而 是單位矩陣，則描述上述線性變換的是 豪斯霍爾德矩陣（ 表示向量 的共軛轉置）

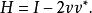householder變換

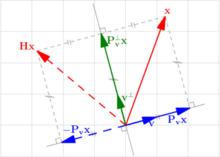圖1.豪斯霍爾德變換示意圖

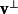householder變換

豪斯霍爾德變換示意圖：向量 x在豪斯霍爾德向量v的超平面 上的鏡像是 Hx， H是豪斯霍爾德矩陣。

例：2維平面

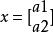householder變換

我們設 ,則有下式：

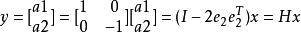householder變換

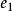householder變換

householder變換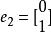

householder變換

其中 和 是單位向量。 ，是正交矩陣，且detH=-1。

性質

householder變換矩陣有如下性質:

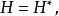householder變換

1）它是埃爾米特矩陣：

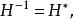householder變換

2）它是正交矩陣：

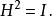householder變換

3）因此也是對合的：

householder變換

householder變換

householder變換

進一步的， 實際上按上面描述的那樣反射了點 (用它的位置向量 來識別)，因為

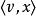householder變換

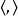householder變換

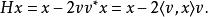householder變換

這裡的 表示點積。注意等於從 X到超平面的距離。

套用

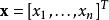householder變換

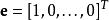householder變換

householder變換可以將向量的某些元素置零，同時保持該向量的範數不變。例如，將非零列向量 變換為單位基向量 的豪斯霍爾德矩陣為

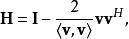householder變換

householder變換

其中householder向量 滿足：

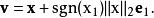householder變換

Dubrulle 在2000年給出了將豪斯霍爾德變換套用於生成一個一般的稀疏向量的一個數值穩定的算法。

對一個矩陣的各個列向量逐一進行相應的豪斯霍爾德變換，可以將這個矩陣變換為上海森伯格矩陣、上三角矩陣等形式。後者就是QR分解的豪斯霍爾德算法 。