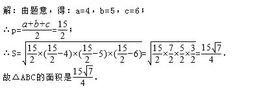人物簡介
Heron 海倫生於公元10年到公元75年
海倫他是一個非常重要的幾何學家和機械學家,他生長在這個對數學家生平不是很注重的年代,以致於雖然有一些文章是以海倫為名,但是後人還是不敢肯定是否真的是海倫本人所著。要確定海倫真正的出生年月日是非常困難的,一派的人認為他出生於公元前150年左右,另一派的人則認為他出生於公元後250年,前一派人的主張是基於目前並未發現有比阿基米得更晚的海倫作品,而後一派的人則認為他生長於托勒密之後,所以應該是公元後才對。
可是最近又有第三種證據顯示,以上兩種說法都是錯誤的,因為有一個跟他同時代的詩人柯南美拉,他是一位羅馬士兵,曾在一篇文章中提過他,史學家也在1938年,找到其他證據支持這個論點。從他的著作中我們知道他曾經在亞歷山大博物館工作過,在那裡他傳授幾何、物理、氣體學和機械學,上課的內容有一些是他著作的教科書,有一些他的草稿。
研究領域
他的書可分成兩類,一類是理論的部分,包括了幾何、算數、天文學和物理,另一類是則是技能指南的部分,包括了物質學、建築學、木工和生活上使用到之技巧。大量的海龍的著作已經被發現,儘管有些地方對於是否真的是海龍本人所著還有爭議,在書上的天文學一篇文章說,如何利用月來測量亞歷山大城到羅馬城,在氣體學的部分如何利用空氣、河流和水壓來作機械的用途,並運用到戰場上,在物理學上,他也會利用槓桿、滑輪、階梯或螺鏇來撐起重物,並考慮物體的中心等問題。在數學上,他已經會求三角形和正方形的面積,知道邊數是3到12的正多面體種類,錐和柱的表面積算法,並且他已經會算平方根的近似值了,事實上他也找出了從1到100所有的數的立方根,當然海倫最著名的當然是他證明了他的''海倫公式''。
個人著作
希臘的數學家與測量學家,大約生於西元75年左右,他在數學方面最能代表其成就的著作是度量論(Metrica)一書,該書的原稿本於1896年才被發現,全書共分為三卷.第一卷由矩形和三角形開始,討論了平面圖形和立體表面之面積,並給出了著名的三角形面積公式-海龍公式.第二卷探討立體圖形,其中包括圓錐體,圓柱體,稜柱體等立體體積的求法.第三卷介紹了平面和立體圖形案給定比例之分割,並用到了求立方根的近似公式.
海倫另一部關於測地學的著作(Dioptra)也很有名,在這部著作中,海倫對如何在隧道之兩端同時動工而能使之銜接提出說明,也解釋如何測量兩地的距離,包括有一地不能到達以及兩地均能看見但均不能到達的情形;另外他也說明如何從已知點到不可及的一線作垂線,以及如何測知一塊地的面積而不需進入這塊地面上.大家熟知的三角形面積公式(a,b,c為三角形之三邊長,s為周長之半),是最後提到的觀念(不進入一塊地而能測知其面積的依據).這個公式出現於他的測地學(Deodesy),在Dioptra和Metrica中又再度出現,並且附上證明.海龍的著作之特色是摻合了嚴密數學和近似方法以及埃及人的公式,海倫所提出的公式有許多並未附上證明而一部份的公式則只給岀近似值而已.除了上述正確的三角形面積公式,他另外提出一個不精確的三角形面積公式.
成就
海龍之所以提出許多埃及時代的公式(例如以做為之近似值),可能原因之一是精確公式所涉及的平方根,立方根等,並不是測量人員所用的上的;事實上,純幾何與測地學或度量學還是有些不同,測地學中求面積和體積的方法並不屬於高等教育的範圍,它們只教給測量員,泥水匠,木匠和技術人員.無疑的,海倫繼承埃及的測量科學並加以發揚光大,他的測地學著作被沿用了好幾百年.