Tanner圖發展背景
低密度校驗(Low Density Parity Check, LDPC)碼是一種基 於稀疏矩陣的奇偶校驗碼。 Gallager 於1962年首先發現了這種碼,故又稱Gallager碼。由於當時的計算機處理能力與相關理論的薄弱,這種優秀的碼並沒有在科學界引起足夠的重視。
1981年,Tanner提出了用 圖模型來描述碼字的概念,從而將LDPC碼的校驗矩陣對應到被成為Tanner圖的 雙向二部圖上,採用Tanner 圖構造的LDPC碼,通過並行解碼可以顯著地降低解碼複雜度。
1993年Turbo碼的問世與成功使Mackay、Neal、Spielman和Sipser等 “又重新提出了”LDPC碼。Mackay和Neal利用 隨機構造的Tanner圖研究了LDPC碼的性能,發現採用和積解碼算法的正則LDPC碼具有和Turbo碼相似的解碼性能,在長碼時甚至超過了Turbo碼。Spielman和Sipser提出了基於二部擴展圖的擴展碼。在對擴展碼的研究中,他們證明了一個隨機構造的 Tanner圖以很大的機率為好的擴展圖,而由好的擴展圖構造的線性糾錯碼是漸進好碼,從而證明了採用隨機Tanner圖構造的LDPC碼以很大機率是漸進好碼。
Tanner圖簡介
Tanner圖是由Mr Tanner在1981在論文中提出來的,是研究低密度校驗碼的重要工具。
Tanner圖表示的是 LDPC 的校驗矩陣。Tanner圖中的循環是由圖中的一群相互連線在一起的頂點所組成的。循環以這群頂點中的一個同時作為起點和終點,且只經過每個頂點一次。循環的長度定義為它所包含的連線的數量;而圖形的圍長,也成為圖形的尺寸,定義為圖中最小的循環長度。
Tanner圖包含兩類頂點: n個碼字比特頂點(稱為比特頂點),分別與校驗矩陣的各列對應; m個校驗方程頂點(稱為校驗節點),分別與校驗矩陣的各行對應。校驗矩陣的每行表示一個校驗方程,每列代表一個碼字比特。 如果一個碼字比特包含在相應的校驗方程中,那么就用一條連線將所涉及的比特節點和校驗節點連起來,所以Tanner圖中的連線數與校驗矩陣中的1的個數相同。 比特節點用圓形節點表示,校驗節點用方形節點表示。
Tanner圖表示方式
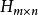 Tanner圖
Tanner圖 Tanner圖
Tanner圖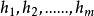 Tanner圖
Tanner圖 Tanner圖
Tanner圖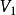 Tanner圖
Tanner圖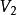 Tanner圖
Tanner圖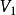 Tanner圖
Tanner圖 Tanner圖
Tanner圖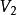 Tanner圖
Tanner圖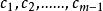 Tanner圖
Tanner圖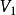 Tanner圖
Tanner圖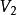 Tanner圖
Tanner圖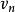 Tanner圖
Tanner圖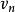 Tanner圖
Tanner圖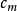 Tanner圖
Tanner圖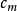 Tanner圖
Tanner圖 Tanner圖
Tanner圖 Tanner圖
Tanner圖 Tanner圖
Tanner圖 Tanner圖
Tanner圖校驗矩陣 表示長度為n的線性分組碼, 中有m個行向量 。構造一個圖 ,它由兩個節點集合構成,分別是 和。由代表n-1個碼字比特的節點組成,記為稱為變數(Variable)節點。由表示m-1個校驗方程的節點構成,記為稱為校驗節點。和本身不存在直接相連的邊,任意一邊分別連線著某一個校驗節點和某一個變數節點,稱這種圖為二分圖(Bipartite Graph),即Tanner圖。在Tanner圖中定義一個節點的度數為與這個節點相連線的邊個數。因此,變數節點的度數等於包含的校驗和的個數;校驗節點的度數等於被校驗的變數節點的個數。若校驗矩陣中第行第列元素為非零元,那么在Tanner圖中對應的第個變數節點和第個校驗節點之間就會有一條邊相連。
 Tanner圖
Tanner圖 Tanner圖
Tanner圖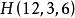 Tanner圖
Tanner圖對於規則的LDPC碼,對應的Tanner圖中全部變數節點的度數都相同並且等於的列重量,全部的校驗節點度數都相同且等於的行重量,如圖1所示為LDPC規則嗎的校驗矩陣所對應的Tanner圖。
 圖1 (12,3,6)LDPC碼校驗矩陣對應的Tanner圖
圖1 (12,3,6)LDPC碼校驗矩陣對應的Tanner圖