基本介紹
在社會或經濟活動中,兩個或多個實體,例如個人、公司、國家等,相互合作結成聯盟或者利益集團,通常能得到比他們單獨活動時獲得更大的利益,產生一加一大於二的效果。然而,這種合作能夠達成或者持續下去的前提就是,合作各方能夠在合作的聯盟中得到他應有的那份利益。那么,如何才能做到合理地分配合作各方獲得的利益呢?我們先來看一個簡單的例子。
【問題1】 甲、乙、丙三人合作經商。倘若甲、乙合作可獲利7萬元,甲、丙合作可獲利5萬元,乙、丙合作可獲利4萬元,三人合作則獲利10萬元,每人單幹各獲利1萬元。問三人合作時如何分配獲利?
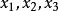 Shapley值法
Shapley值法很顯然,利益分配時,三人獲利總和應為10萬元。設甲、乙、丙三人分配獲利為,則有
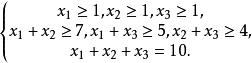 Shapley值法
Shapley值法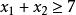 Shapley值法
Shapley值法三人中如果誰獲利小於1萬元,則他就會單幹,不會加入這個聯盟。如果不成立,甲和乙就會組成一個小的聯盟,而把丙拋在一邊。
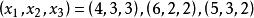 Shapley值法
Shapley值法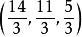 Shapley值法
Shapley值法但是,這個系統有無窮多組解,例如,甚至是(3,5,2)。很顯然,站在乙或丙的角度,和甲合作都可以獲得更大的利益,換言之,甲在他所參與的合作中貢獻最大;同理,乙次之,丙貢獻最小。因此,像(5,3,2),都是合理的解。哪一個更合理?因此應該有一種圓滿的利益分配方法。
這類問題稱為 n人合作對策。L.S.Shapley在1953年給出了解決該問題的一種方法,稱為 Shapley值法。
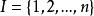 Shapley值法
Shapley值法 Shapley值法
Shapley值法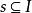 Shapley值法
Shapley值法下面先給出 合作對策的一般模型。記為n個合作人的集合。若對於的任何子集都有一個實數v(s)與之對應,且滿足下列條件:
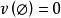 Shapley值法
Shapley值法 Shapley值法
Shapley值法(1),其中為空集。
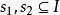 Shapley值法
Shapley值法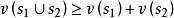 Shapley值法
Shapley值法 Shapley值法
Shapley值法(2)對於任意兩個不交子集,都有,則稱v(s)為定義在上的一個特徵函式。
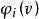 Shapley值法
Shapley值法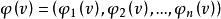 Shapley值法
Shapley值法在實際問題中,v(s)就是各種聯盟的獲利,而第二個條件表明任何情況下合作至少總比單幹或者小團體的合作來得有利。 合作對策就是需要確定每個人獲得的利益,或者對全體成員來講就是向量。按照前例的分析,我們知道合理的分配需要滿足
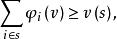 Shapley值法
Shapley值法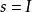 Shapley值法
Shapley值法並且,該式當時等號成立。
上述的提法中實質上沒有什麼限制,這樣我們總可以找到多個解。所以,必須有一些有關合理性的限制,在諒限制下,尋找合理的對策才是有意義的。
Shapley給出了一組對策應滿足的公理,並證明了在這些公理下合作對策是唯一的。
 Shapley值法
Shapley值法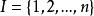 Shapley值法
Shapley值法 Shapley值法
Shapley值法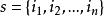 Shapley值法
Shapley值法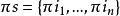 Shapley值法
Shapley值法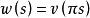 Shapley值法
Shapley值法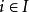 Shapley值法
Shapley值法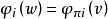 Shapley值法
Shapley值法【公理1】( 對稱性)設是的一個排列,對於的任意子集,有。若在定義特徵函式,則對於每個都有。
這表示合作獲利的分配不隨每個人在合作中的記號或次序變化。
【公理2】( 有效性)合作各方獲利總和等於合作獲利:
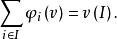 Shapley值法
Shapley值法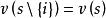 Shapley值法
Shapley值法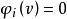 Shapley值法
Shapley值法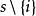 Shapley值法
Shapley值法【公理3】( 冗員性)若對於包含成員i的所有子集s都有,則。其中為集合s去掉元素i後的集合。
這說明如果一個成員對於任何他參與的合作聯盟都沒有貢獻,則他不應當從全體合作中獲利。
 Shapley值法
Shapley值法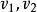 Shapley值法
Shapley值法【公理4】( 可加性)若在上有兩個特徵函式,則有
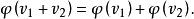 Shapley值法
Shapley值法這表明有多種合作時,每種合作的利益分配方式與其他合作結果無關。
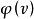 Shapley值法
Shapley值法Shapley證明了滿足這四條公理的是唯一的,並且其公式為
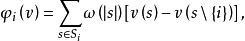 Shapley值法
Shapley值法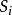 Shapley值法
Shapley值法 Shapley值法
Shapley值法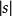 Shapley值法
Shapley值法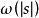 Shapley值法
Shapley值法其中,是中包含成員i的所有子集形成的集合,是集合s元素的個數,是加權因子且有
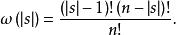 Shapley值法
Shapley值法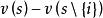 Shapley值法
Shapley值法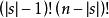 Shapley值法
Shapley值法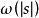 Shapley值法
Shapley值法Shapley值公式可以解釋如下:是成員i在他參與的合作s中做出的貢獻。這種合作的總計有出現的方式,因此每一種出現的機率就是。
程式表達
Shapley值法寫成程式就是:
function shapley
n= input(’Number of cooperators:’);
for j=1:n,
nam{j}=input (['Name of cooperator' num2str(j)’:’] ,’s’);
end
for k =1:2^n-1,
w{k}=abs (dec2bin(k)- 48);
w{k}= [zeros(1,n-length(w{k})) w{k}];
fprintf ('The profit for cooperator’);
for j= I:n,
if w{k}(j)==1,
fprintf(’% s', nam{j});
end
end
p(k)=input(’:’);
end
fprintf ('\nIf they cooperate,then \n');
for j=1:n,
x(j)=1/n*p(2^(n-j));
for k =1:2^n-1,
if w{k}(j)==0,
s = sum(w{k})+ 1;
ww =1/s/nchoosek(n,s);
x(j)=x(j)+ww* (p(k+2^(n-j))一p(k));
end
end
fprintf ('The profit for % s is : % f. \n, nam{j},x(j));
end

