Riccati方程

簡介

黎卡提方程是最簡單的一類非線性方程。形如y'=P(x)y +Q(x)y+R(x)的方程稱為黎卡提方程。

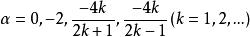Riccati方程

對其特例y'=-by +cx ，劉維爾(Liouville,J.)於1941年證明了：若且唯若時，方程才能求得用初等函式及其積分所表示的通解。劉維爾的工作使得人們的注意力開始轉向微分方程解的定性研究、數值計算以及求近似解上。

發展

十七世紀，義大利數學家黎卡提提出如下方程：dy/dx=P(x)y +Q(x)y+R(x)，稱為黎卡提方程。

1841年法國數學家劉維爾證明了黎卡提(Riccati)方程一般沒有初等解法，但是很多實際問題與理論問題又迫切需要求得這個方程的解，這也使得這一方程成為世界著名難題。

黎卡提方程自從十七世紀黎卡提提出以來，歷經三百多年一直未有一般解法，雖然有眾多特例解法，但是都未能從根本上解決這個方程。

套用

無論在微分方程的經典理論或在近代科學的有關分支，黎卡提方程均有重要套用。