Pólya定理
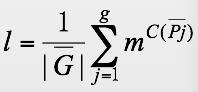Pólya定理 ·設G={P1,P2,…,Pg}是n個對象的一個置換群 ，C(Pk)是置換Pk的循環的個數，用m種顏色對n個對象著色,著色方案數為
Burnside引理
設G={a1,a2,…ag}是目標集[1,n]上的置換群。每個置換都寫成不相交循環的乘積。G將[1,n]劃分成l個等價類.c1(ak)是在置換ak的作用下不動點的個數。
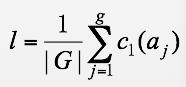Pólya定理 比較Pólya定理 和Burnside引理
–Pólya定理中的群G是作用在n個對象上的置換群
–Burnside引理中的群G是對這n個對象染色後的方案集合上的置換群
-兩個群之間的聯繫：群G的元素，相應的在染色方案上也誘導出一個屬於G的置換
例題
問：甲烷CH4的4個鍵任意用H(氫),Cl(氯),CH3(甲基),C2H5(乙基)連線，有多少種方案？
答：
CH4的結構是一個空間正4面體，C原子居於正4面體的中心。
正4面體的轉動群按轉動軸分類：
·不動旋轉: （A)(B)(C)(D) 共有1個(1)4循環
·以頂點與對面的中心連線為軸按反時針方向旋轉±120度。置換(BCD)與(BDC)。置換(ACD)與(ADC)，置換(ABD)及(ADB)，(ABC)及(ACB )所對應的旋轉。共有8個(1)1(3)1循環。
·以正四面體的3對對邊之中點聯線為旋轉軸旋轉180度: (AB)(CD)，(AC)(BD)，(AD)(BC),共有3個(2)2循環
由Pólya定理有 (1*4 +8*4 +3*4 )/12=36
