Polya定理(數學)
Redfield-Polya (Pólya enumeration theorem,簡稱PET)定理是組合數學理論中最重要的定理之一.自從 1927 年 Redfield 首次運用 group reduction function 概念,現在稱之為群的循環指標(circle index of a group),至今 60 多年來,他在許多實際計數問題上得到了廣泛的套用,它以置換群為理論基礎,與生成函式有機地結合在一起,揭示了一類具有組合意義的計數的規律性.
抽象地說在一集合內,定義了一個等價關係,人們往往關心由這個等價關係所決定的等價類的數目,Refield-Polya 理論就是為解決這類問題而發展起來的複雜計數理論.
1 置換群的基本概念
置換的定義:
置換即[1,n]到自身的1-1變換: [1,n] → [1,n],
 Polya
Polya Polya
Polya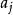 Polya
Polyap: i → , ( ≠ , i ≠ j)
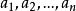 Polya
Polya於是, 是[1,n] 的一個全排列。稱此置換為n階置換,記為
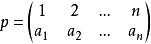 Polya
Polyan階置換共有n!個。
置換的乘法運算:
先看一個例子,設:
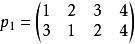 Polya
Polya Polya
Polya,
定義
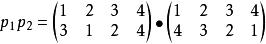 Polya
Polya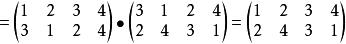 Polya
Polya這表示先作p1的置換,再作p2的置換:
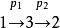 Polya
Polya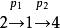 Polya
Polya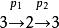 Polya
Polya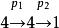 Polya
Polya故
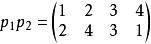 Polya
Polya類似的有
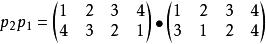 Polya
Polya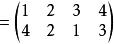 Polya
Polya於是我們定義乘法如下:
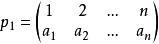 Polya
Polya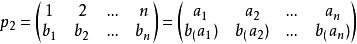 Polya
Polya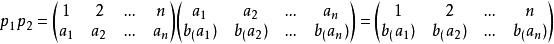 Polya
Polya定理 [1,n]上所有的置換按上述乘法構成一個群。即滿足
1)封閉性
2)結合律
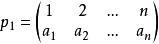 Polya
Polya3)有單位元
4)有逆元
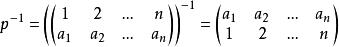 Polya
Polya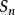 Polya
Polya我們稱此群為n個文字的對稱群,記為
定義:Sn的任意一個子群稱為置換群
定理: 任一n階有限群同構於一個n個文字的置換群
設G={a1,a2,…,an},指定G中任一元ai, 任意aj∈G,
Pi:aj → aj ai ,則Pi是G上的一個置換。
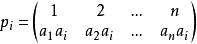 Polya
Polya令P={Pi|ai∈G},則P≈G
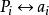 Polya
Polya1-1映射:
2 Polya定理
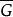 Polya
Polya設 是n個對象的一個置換群, 用m種顏色染圖這n個對象,則不同的染色方案數為:
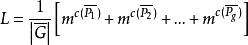 Polya
Polya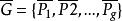 Polya
Polya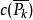 Polya
Polya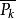 Polya
Polya其中 , 為 的循環節數
證明
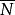 Polya
Polya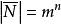 Polya
Polya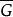 Polya
Polya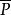 Polya
Polya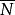 Polya
Polya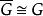 Polya
Polya設 是N中元素所有染色方案的集合,則有 。對於 中任意一個置換 ,由於它作用於N中的元素,從而也引起了對於 中塗色方案的置換P。記所有P構成的群為G,則
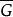 Polya
Polya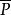 Polya
Polya設是中的一個置換,且
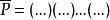 Polya
Polya↑
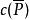 Polya
Polya{ 個輪換}
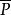 Polya
Polya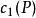 Polya
Polya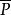 Polya
Polya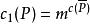 Polya
Polya如果屬於同一輪換的的數字被塗上同樣的顏色,這樣的塗色方案在P的作用下是不變的,所以它屬於P的不變元素。另一方面,如果有一種塗色方案使得得 某個輪換中出現了不同的塗色,則在該輪換中必有兩個相連的數字具有不同的顏色,於是在P的作用下必得到不同的塗色方案,這就證明了在P作用下不變的塗色方案數 應該等於對 的同一輪換塗同色的方案數 ,即,將將此式代 入Burnside 引理即得結論。
套用(正多面體的剛體旋轉問題)
甲烷CH4的支鏈結構為正四面體,若4個H鍵用H,CL,CH3,C2H5之一取代,問有幾種不同的化學結構?
解:
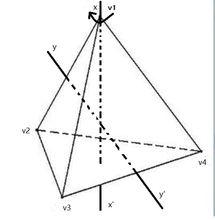 Polya
Polya問題相當於對正四面體的4個頂點用4種顏色著色,求不同的方案數目,使正四面體v1,v2,v3,v4重合的剛體運動有兩類,一類是繞過頂點的中心線XX'旋轉120度,240度;另一類是繞過v1v2,v3v4中點的連線yy’旋轉180度,如下圖旋轉群G的元素為:
(v1)(v2)(v3)(v4),(v1)(v2v3v4),(v1)(v4v3v2),(v2)(v1v3v4),
(v2)(v4v3v1),(v3)(v1v2v4),(v3)(v4v2v1),(v4)(v1v2v3),
(v4)(v3v2v1),(v1v2)(v3v4),(v1v3)(v2v4),(v1v4)(v2v3),
故不同的化學結構數目為:
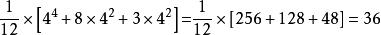 Polya
PolyaPolyA(多聚腺苷酸)
解釋
多聚腺苷酸化
是指多聚腺苷酸與信使RNA(mRNA)分子的共價鏈結。在蛋白質生物合成的過程中,這是產生準備作翻譯的成熟mRNA的方式的一部份。在真核生物中,多聚腺苷酸化是一種機制,令mRNA分子於它們的3'端中斷。多聚腺苷酸尾(或聚A尾)保護mRNA,免受核酸外切酶攻擊,並且對轉錄終結、將mRNA從細胞核輸出及進行翻譯都十分重要。一些原核生物的mRNA都會被多聚腺苷酸化,但多聚腺苷酸尾的功能則與真核生物有所不同。
當脫氧核糖核酸(DNA)在細胞核內轉錄成核糖核酸(RNA)的過程中及完成後,多聚腺苷酸化就會出現。當轉錄停止後,mRNA鏈會由核酸外切酶及RNA聚合酶切開。切開位點的附近有著AAUAAA序列。當mRNA被切開後,會加入50-250個腺苷到切開位點的3'端上。這個反應是由多聚腺苷酸聚合酶參與完成的。
多聚腺苷酸化過程
1,切割及多聚腺苷酸化特異因子(CPSF)及切割活化因子(CstF)兩個蛋白質複合物會開始與末端的RNA聚合酶Ⅱ結合。
2,當RNA聚合酶Ⅱ前進時經過多聚腺苷酸化信號序列的CPSF,及CstF轉移至新的mRNA前體,CPSF會與AAUAAA序列結合,而CstF會與其後3的GU序列或充滿U的序列結合。
4,CPSF及CstF會在約AAUAAA序列後35個核苷啟動切割。多聚腺苷酸聚合酶(PAP)會立即展開編寫多聚腺苷酸尾。細胞核內的多聚腺苷酸結合蛋白(PABPN1)會立即與新的多聚腺苷酸序列結合。
5,CPSF會開始游離,而PAP會繼續多聚腺苷酸化及編寫約50-250個核苷(視乎生物的品種)的腺苷尾。PABPN1會成為一種分子尺,界定多聚腺苷酸化何時停止。 PAP會開始游離,及PABPN1繼續維持結合狀態。連同5'端帽,這相信是可以幫助mRNA運離細胞核。
內部連結
相關的蛋白質及複合物:
RNA聚合酶
RNA聚合酶Ⅱ
相關的化合物有:
腺苷
加A反應
