發現者信息
奧古斯特·費迪南德·莫比烏斯(August Ferdinand Möbius,1790年11月17日-1868年9月26日),德國數學家和天文學家,被認為是拓撲學的先驅。
出生於德國薩克森-安哈特舒爾佛特。莫比烏斯最初學法學,1809年轉向數學。從1809年到1814年他在萊比錫大學學數學並獲博士學位。1815年他獲得教授資格,一年後在高斯的推薦下成為特級教授和萊比錫天文台的觀測員。1846年他成為王家薩克森科學院建立成員之一。1848年他成為萊比錫天文台台長。1868年9月26日逝世於萊比錫。
莫比烏斯最著名的成就是發現了三維歐幾里得空間中的一種奇特的二維單面環狀結構——後人稱為莫比烏斯帶。其他重要的成就包括在射影幾何中引進齊次坐標系、莫比烏斯變換(Möbius transformations),數論中的莫比烏斯變換、莫比烏斯函式、莫比烏斯反演公式等等。
定義
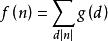 Mobius反演定理
Mobius反演定理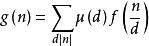 Mobius反演定理
Mobius反演定理f(n)和g(n)是定義在正整數集合上的兩個函式,若
則反之亦然。
其中
μ(d)=1, 若d=偶數個不同素數之積
μ(d)=(-1), 若d=奇數個不同素數之積
μ(d)=0, 其他
例如:
μ( 30) = μ( 2·3·5 ) = (-1)
μ(12) = μ( 3·2 ) = 0
對任何素數p,μ(p)=-1
輔助定理
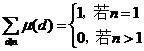 Mobius反演定理
Mobius反演定理對於任意正整數n,恆有
其中,d|n表示取遍n的正整數因子d,例如n=12時,d可以去1,2,3,4,6,12
反演定理證明
 Mobius反演定理
Mobius反演定理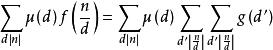 Mobius反演定理
Mobius反演定理 Mobius反演定理
Mobius反演定理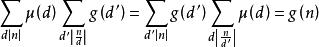 Mobius反演定理
Mobius反演定理根據f(n)的公式可得
所以令n=dd'n1,因
故
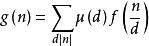 Mobius反演定理
Mobius反演定理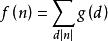 Mobius反演定理
Mobius反演定理反過來類似可證,若
則舉例
 Mobius反演定理
Mobius反演定理f(1)=1, f(2)=1+2=3, f(4)1+2+4=7, f(6)=1+2+3+6=12,
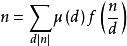 Mobius反演定理
Mobius反演定理根據反演定理,g(n)=n可得
套用舉例
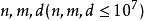 Mobius反演定理
Mobius反演定理 Mobius反演定理
Mobius反演定理給定,求
直接暴力枚舉的複雜度難以接受,考慮使用莫比烏斯反演
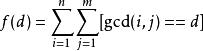 Mobius反演定理
Mobius反演定理 Mobius反演定理
Mobius反演定理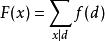 Mobius反演定理
Mobius反演定理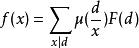 Mobius反演定理
Mobius反演定理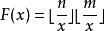 Mobius反演定理
Mobius反演定理 Mobius反演定理
Mobius反演定理注意到可以在的時間內計算出來
 Mobius反演定理
Mobius反演定理所以這個式子求的複雜度得到了簡化,進一步的,通過枚舉商分塊複雜度可以降到根號級別
背後故事
花絮--莫比烏斯帶
 莫比烏斯帶
莫比烏斯帶莫比烏斯帶本身具有很多奇妙的性質。如果從中間剪開一個莫比烏斯帶,不會得到兩個窄的帶子,而是會形成一個把紙帶的端頭扭轉了兩次再結合的環,再把剛剛做出那個把紙帶的端頭扭轉了兩次再結合的環從中間剪開,則變成兩個環。如果你把帶子的寬度分為三分,並沿著分割線剪開的話,會得到兩個環,一個是窄一些的莫比烏斯帶,另一個則是一個旋轉了兩次再結合的環。另外一個有趣的特性是將紙帶旋轉多次再貼上末端而產生的。比如旋轉三個半圈的帶子再剪開後會形成一個三葉結。剪開帶子之後再進行旋轉,然後重新貼上則會變成數個Paradromic。
莫比烏斯帶常被認為是無窮大符號「∞」的創意來源,因為如果某個人站在一個巨大的莫比烏斯帶的表面上沿著他能看到的“路”一直走下去,他就永遠不會停下來。但是這是一個不真實的傳聞,因為「∞」的發明比莫比烏斯帶還要早。

