介紹
k-meansAlgorithm算法是一個聚類算法，把n的對象根據他們的屬性分為k個分割，k<n。它與處理混合
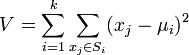K平均算法公式常態分配的最大期望算法很相似，因為他們都試圖找到數據中自然聚類的中心。它假設對象屬性來自於空間向量，並且目標是使各個群組內部的均方誤差總和最小。假設有k個群組Si,i=1,2,...,k。μi是群組Si內所有元素xj的重心，或叫中心點。
發明歷史
k平均聚類發明於1956年，該算法最常見的形式是採用被稱為勞埃德算法(Lloydalgorithm)的疊代式改進探索法。勞埃德算法首先把輸入點分成k個初始化分組，可以是隨機的或者使用一些啟發式數據。然後計算每組的中心點，根據中心點的位置把對象分到離它最近的中心，重新確定分組。繼續重複不斷地計算中心並重新分組，直到收斂，即對象不再改變分組（中心點位置不再改變）。勞埃德算法和k平均通常是緊密聯繫的，但是在實際套用中，勞埃德算法是解決k平均問題的啟發式法則，對於某些起始點和重心的組合，勞埃德算法可能實際上收斂於錯誤的結果。（上面函式中存在的不同的最優解）
雖然存在變異，但是勞埃德算法仍舊保持流行，因為它在實際中收斂非常快。實際上，觀察發現疊代次數遠遠少於點的數量。然而最近，DavidArthur和SergeiVassilvitskii提出存在特定的點集使得k平均算法花費超多項式時間達到收斂。
近似的k平均算法已經被設計用於原始數據子集的計算。
從算法的表現上來說，它並不保證一定得到全局最優解，最終解的質量很大程度上取決於初始化的分組。由於該算法的速度很快，因此常用的一種方法是多次運行k平均算法，選擇最優解。
k平均算法的一個缺點是，分組的數目k是一個輸入參數，不合適的k可能返回較差的結果。另外，算法還假設均方誤差是計算群組分散度的最佳參數。
