定義
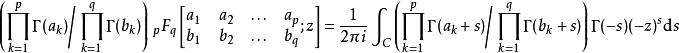 G-函式
G-函式其中積分路徑C視參數p,q的相對大小而定。上面的積分表達式具有Mellin 逆變換的形式。
Meijer-G函式是上面積分表達式的一個推廣,它的定義為:
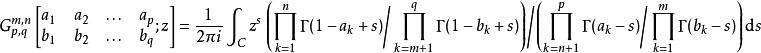 G-函式
G-函式其中積分路徑C視參數的相對大小而定。但是,為了保證至少一條積分路徑有定義,要求
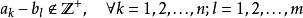 G-函式
G-函式在書寫 Meijer-G函式時要注意,上標中的第一個參數和下標中的第二個參數對應的是b,而上標中的第二個參數和下標中的第一個參數對應的是a。
對比上述兩式可以得到廣義超幾何函式和 Meijer-G函式的關係:
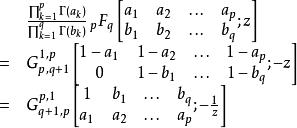 G-函式
G-函式基本性質
和廣義超幾何函式一樣,如果上下兩個向量組在合適的位置有相同的元素,則 Meijer-G函式可以降階,此處不再贅述。
一般關係式
Meijer-G函式的導函式具有下列性質:
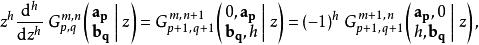 G-函式
G-函式注意h可以取任意整數值,取負數時表示不定積分。
另一方面,
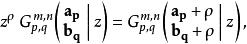 G-函式
G-函式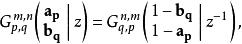 G-函式
G-函式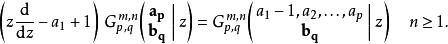 G-函式
G-函式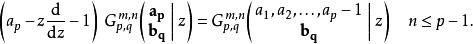 G-函式
G-函式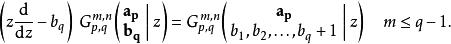 G-函式
G-函式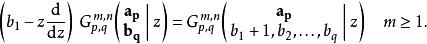 G-函式
G-函式上面的式子都可以直接由定義得到。
向量組中兩個元素相差整數時的關係式
由
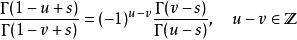 G-函式
G-函式又有
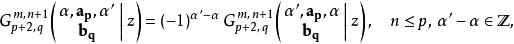 G-函式
G-函式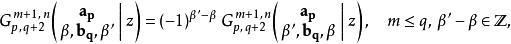 G-函式
G-函式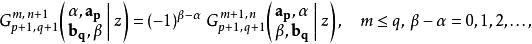 G-函式
G-函式微分方程
由上面一般關係式一節的討論知 Meijer-G函式滿足下列微分方程,它與廣義超幾何函式滿足的微分方程形式上很類似。
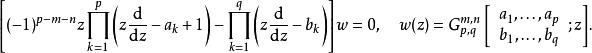 G-函式
G-函式這是一個 max(p,q) 階的線性微分方程,在z=0 附近的基本解組可以選取為
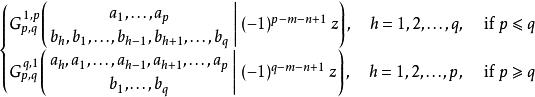 G-函式
G-函式當p=q時兩種取法都可以。
從m,n的取值上就可以看到它們跟廣義超幾何函式有直接的聯繫。事實上的確如此,以第一種情況為例,
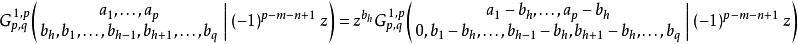 G-函式
G-函式等號右邊的 Meijer-G函式顯然就是廣義超幾何函式。
特殊情形
因為廣義超幾何函式是 Meijer-G函式的特殊情形,故所有可以用廣義超幾何函式表示的特殊函式都可以用 Meijer-G函式表示,但是,在個別情況下,用 Meijer-G函式有更簡單的表示式,例子如諾依曼函式,它可以用超幾何函式F表示,但表示式僅僅是將(第一類)貝塞爾函式的超幾何函式表示式代入其定義式中,因此含有兩個超幾何函式。而用 Meijer-G函式就可以直接表示為 :
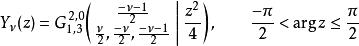 G-函式
G-函式另外一個例子是不完全伽瑪函式對參變數的偏導數,它無法用廣義超幾何函式表出,但可以用 Meijer-G函式表出:
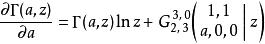 G-函式
G-函式事實上,不完全伽瑪函式對參變數的高階偏導數也可以用 Meijer-G函式表出,詳見不完全Γ函式一文。
