定義
巴尼斯G函式是超級階乘函式在複數上的擴展。
它與Γ函式、K函式以及格萊舍常數（Glaisher constant）有關。
巴尼斯G函式以數學家歐尼斯特·巴尼斯（Ernest William Barnes）的名字命名。
巴尼斯G函式可以通用魏爾施特拉斯分解定理的形式定義為 ：
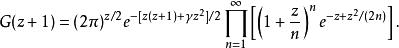巴尼斯G函式其中，γ表示歐拉-馬歇羅尼常數。
差分方程、函式方程與特殊值
巴尼斯G函式滿足差分方程
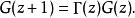巴尼斯G函式特殊地，G(1)=1。
從此方程可推出G取整數自變數時有：
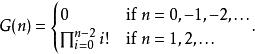巴尼斯G函式因此，
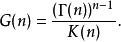巴尼斯G函式
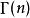巴尼斯G函式
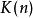巴尼斯G函式其中， 表示Γ函式， 表示K函式。
巴尼斯G函式另外，在滿足條件 時，差分方程唯一確定一個G函式。.
由G函式的差分方程和Γ函式的函式方程可以得到（由Hermann Kinkelin提出）：
巴尼斯G函式乘法公式
與Γ函式一樣，G函式也有其乘法公式：
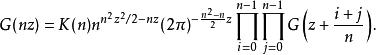巴尼斯G函式 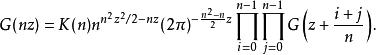巴尼斯G函式其中K是一個常數，定義為：
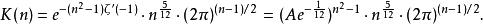巴尼斯G函式
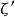巴尼斯G函式其中 表示黎曼ζ函式的導函式， A則表示為格萊舍常數。
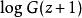巴尼斯G函式可漸近展開為（由巴尼斯提出）：
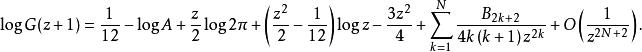巴尼斯G函式
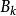巴尼斯G函式
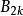巴尼斯G函式
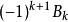巴尼斯G函式其中 為伯努利數，A 為格萊舍常數。（需要注意的是，在巴尼斯的時代，伯努利數習慣寫成。）
