狄克斯特拉算法

狄克斯特拉算法，一譯迪傑斯特拉算法(Dijkstra)，是典型的單源最短路徑算法，用於計算一個節點到其他所有節點的最短路徑。主要特點是以起始點為中心向外層層擴展，直到擴展到終點為止。

簡介算法依據

若從S點到T點有一條最短的路徑，則該路徑上的任何點到S的距離都是最短的。如上圖，A到C的最短路徑為A——E——C，可以看出來其路徑上的一點如E到C的最短距離也在A——E——C這條路徑上。
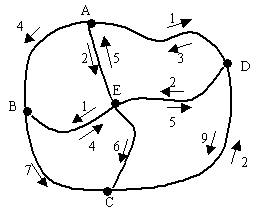
對於這種很簡單的圖我們可以通過窮舉比較法很容易得到最短路徑。但是對於大規模的網路圖，比如大城市的道路網路。這樣的話我們就很難一眼看出來最短路徑了。這時要用計算機根據狄克斯特拉算法計算最短路徑了。

算法的步驟

將所有的頂點分為S,T兩類S用來存放已知最短路徑的頂點。而T存放未知最短路徑的頂點。如果起始點（假設上圖的v1為起始點）到某個頂點（相鄰點）的最短距離已經求出，比如A——B的距離。那么就把B歸入S，其餘的不能直接算出最短距離的則要歸入T。
剛開始的S只有起始點一個，隨著算法的繼續，首先將起始點相鄰的點歸入到S，知道最後一點——目標點歸入S。

在起始點與相鄰點的路徑中選擇一個最短的

然後將這個相鄰點設為起始點，重複上一步（注意，不能回退到第一個起始點，只能遞接下去）。直到所有的點都歸為S為止。

用公式表示如下

另d（x，y）表示點x到y的距離，D（x）表示x到起始點的距離。
對起始點S做標記，且對所有起始點D（x）為無窮大。對所有為做標記的點按以下公式計算距離
D(x)=min(D(X) d(x,y)+D(y))
其中y是最後一個標記的點。也就是與起始點的距離已知的那個點。
上述這個公式的表示，D(X)要和D（x，y）+D（y）相比，如果前者小，那么就將這個標記點y去掉。路徑直接為起始點到x。否則，路徑要經過y。

套用舉例

如上圖，通過狄克斯特拉算法求出v1到v7的最短距離

一

首先將A做為起始點進行標記。算出v1到相鄰各點的距離。
D(B)=4
D(C)=∞
D(D)=1
D(E)=2
最小值為D(D)=1，所以將D點做標記。

二

因為D(D)最小，所以將D進行標記，重複上個步驟。來計算D(B),D(C),D(E)
D(B)=min(D(B),d(D,B)+D(D))=min(4,∞+1)=4
其中D(B)表示起始點A到B的距離。用這個距離跟起始點A經過D再到B的距離d(D,B)+D(D)相比，如D(B)比較小，則捨棄D點，路徑將不經過D點。這是理解算法的關鍵。
同理得D(C)=min(D(C),d(D,C)+D(D))=min(∞,9+1)=10
D(E)=min(D(E),d(D,E)+D(D))=min(2,2+1)=2
這裡D（E）最小，所以取E點為標記點。且因為起始點A到E的距離比A——D——E的短，所以將D點捨去。

三

對E做標記，計算D(B),D(C)
D(B)=min(D(B),d(E,B)+D(E))=min(4,1+2)=3
D(C)=min(D(C),d(E,C)+D(E))=min(10,6+2)=8
最小值為D(B)=3。去B為標記點，且因為A——E——B的距離比A——B的距離短，所以將E點保留。

四

對B作標記，計算D(C)
D(C)=min(D(C),d(B,C)+D(B))=min(8,7+3)=8
因為D(C)小於d(B,C)+D(B),所以將B點捨去。
綜上，路徑為A——E——C