定義
代數
 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數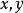 Banach代數
Banach代數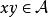 Banach代數
Banach代數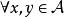 Banach代數
Banach代數定義1 設 是一個線性空間,稱 是一個代數,若:對 中任意兩個元素 ,規定乘積 ,滿足對 和任意數a,有
(1)結合律 x(yz)=(xy)z;
(2)分配律 x(y+z)=xy+xz,(x+y)z=xz+yz;
(3)a(xy)=(ax)y=x(ay).
 Banach代數
Banach代數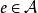 Banach代數
Banach代數註:1)設 是一個代數 ,如果存在 ,使得
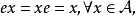 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數就稱 是代數 的一個 單位元。
 Banach代數
Banach代數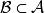 Banach代數
Banach代數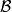 Banach代數
Banach代數 Banach代數
Banach代數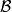 Banach代數
Banach代數 Banach代數
Banach代數2)設 是一個代數,如果 ,且 按 的線性運算及乘法仍是一個代數,則稱 是 的一個 子代數。
 Banach代數
Banach代數 Banach代數
Banach代數3)設 是一個代數 ,當 有單位元時,單位元必是唯一的。
 Banach代數
Banach代數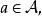 Banach代數
Banach代數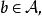 Banach代數
Banach代數4)設 是一個有單位元的代數, 且存在 使得
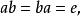 Banach代數
Banach代數 Banach代數
Banach代數其中e為 的單位元,則稱b為a的 逆。
賦范代數
 Banach代數
Banach代數定義2 設 是一個賦范線性空間,同時又是一個代數,而且
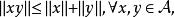 Banach代數
Banach代數 Banach代數
Banach代數則稱 是一個賦范代數。
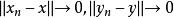 Banach代數
Banach代數註:在賦范代數中,關於乘積範數的性質保證了乘法運算的連續性。實際上,當 時,
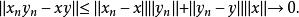 Banach代數
Banach代數Banach代數
定義3 完備的賦范代數稱為Banach代數。
舉例
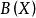 Banach代數
Banach代數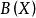 Banach代數
Banach代數例1 設X是賦范線性空間,則 (由X到X的有界線性運算元全體)是一個有單位元的賦范代數,X上的恆等運算元I 即為其單位元。當X為Banach空間時, 是Banach代數。
例2 設X是Banach空間, ,
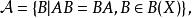 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數即 是與A可交換的有界線性運算元全體,顯然, 是B(X)的一個子代數,而且是閉的,因而也是一個Banach代數。
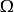 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數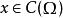 Banach代數
Banach代數例3 設 是緊拓撲空間, 表示 上連續函式全體,對 ,令
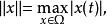 Banach代數
Banach代數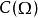 Banach代數
Banach代數則 是一個Banach代數。
譜與譜半徑
對於有限維線性空間上的線性變換,特徵值是一個十分重要的概念。這個概念拓廣到一般的Banach代數中,就是元素的譜。(這裡討論的Banach代數是指復Banach代數。)
 Banach代數
Banach代數 Banach代數
Banach代數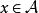 Banach代數
Banach代數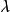 Banach代數
Banach代數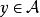 Banach代數
Banach代數定義4 設 是具有單位元 的Banach代數, , 為複數,如果存在 ,使得
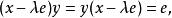 Banach代數
Banach代數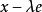 Banach代數
Banach代數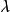 Banach代數
Banach代數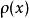 Banach代數
Banach代數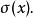 Banach代數
Banach代數即 可逆,則稱 為x的正則點,稱x的正則點全體為正則集,記作 ;稱非正則點為 x的 譜點,稱x的譜點全體為 x的 譜集,記作
 Banach代數
Banach代數 Banach代數
Banach代數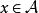 Banach代數
Banach代數定義5 設 是具有單位元 的Banach代數, ,記
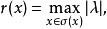 Banach代數
Banach代數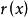 Banach代數
Banach代數稱 為x的 譜半徑。
Banach代數的重要性質
 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數定理1 設 是具有單位元 的Banach代數,則 中可逆元全體是開集,且映射
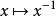 Banach代數
Banach代數在可逆元集合上連續。
 Banach代數
Banach代數 Banach代數
Banach代數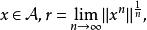 Banach代數
Banach代數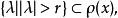 Banach代數
Banach代數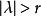 Banach代數
Banach代數定理2 設 是具有單位元 的Banach代數, 則 當 時,
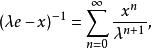 Banach代數
Banach代數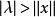 Banach代數
Banach代數且當 時,
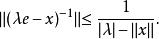 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數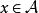 Banach代數
Banach代數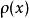 Banach代數
Banach代數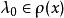 Banach代數
Banach代數定理3 設 是具有單位元 的Banach代數, ,則 是開集。對 ,記
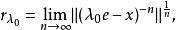 Banach代數
Banach代數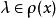 Banach代數
Banach代數則當 時 ,且
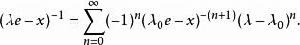 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數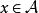 Banach代數
Banach代數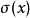 Banach代數
Banach代數定理4 設 是具有單位元 的Banach代數, ,則 是閉集,且
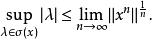 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數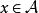 Banach代數
Banach代數定理5 設 是具有單位元 的Banach代數, ,則譜半徑
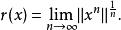 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數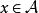 Banach代數
Banach代數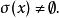 Banach代數
Banach代數定理6 設 是具有單位元 的Banach代數, ,則
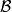 Banach代數
Banach代數 Banach代數
Banach代數 Banach代數
Banach代數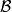 Banach代數
Banach代數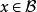 Banach代數
Banach代數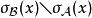 Banach代數
Banach代數定理7 設 是Banach代數 的閉子代數, 、 有相同的單位元, ,則 為開集。
註:定理1-7的證明見參考文獻[1]的59-64頁。
