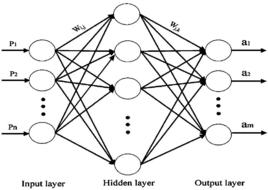
原理
BP算法由信號的正向傳播和誤差的反向傳播兩個過程組成。
正向傳播時,輸入樣本從輸入層進入網路,經隱層逐層傳遞至輸出層,如果輸出層的實際輸出與期望輸出(導師信號)不同,則轉至誤差反向傳播;如果輸出層的實際輸出與期望輸出(導師信號)相同,結束學習算法。
反向傳播時,將輸出誤差(期望輸出與實際輸出之差)按原通路反傳計算,通過隱層反向,直至輸入層,在反傳過程中將誤差分攤給各層的各個單元,獲得各層各單元的誤差信號,並將其作為修正各單元權值的根據。這一計算過程使用梯度下降法完成,在不停地調整各層神經元的權值和閾值後,使誤差信號減小到最低限度。
權值和閾值不斷調整的過程,就是網路的學習與訓練過程,經過信號正向傳播與誤差反向傳播,權值和閾值的調整反覆進行,一直進行到預先設定的學習訓練次數,或輸出誤差減小到允許的程度。
基本思想
BP算法的基本思想是,學習過程由信號的正向傳播與誤差的反向傳播兩個過程組成。正向傳播時,輸入樣本從輸入層傳入,經各隱層逐層處理後,傳向輸出層。若輸出層的實際輸出與期望的輸出(教師信號)不符,則轉入誤差的反向傳播階段。誤差反傳是將輸出誤差以某種形式通過隱層向輸入層逐層反傳,並將誤差分攤給各層的所有單元,從而獲得各層單元的誤差信號,此誤差信號即作為修正各單元權值的依據。這種信號正向傳播與誤差反向傳播的各層權值調整過程,是周而復始地進行的。權值不斷調整的過程,也就是網路的學習訓練過程。此過程一直進行到網路輸出的誤差減少到可接受的程度,或進行到預先設定的學習次數為止。
學習過程
BP算法最早由Werbos於1974年提出,1985年Rumelhart等人發展了該理論。BP網路採用有指導的學習方式,其學習包括以下4個過程。
(1)組成輸入模式由輸入層經過隱含層向輸出層的“模式順傳播”過程。
(2)網路的期望輸出與實際輸出之差的誤差信號由輸出層經過隱含層逐層休整連線權的“誤差逆傳播”過程。
(3)由“模式順傳播”與“誤差逆傳播”的反覆進行的網路“記憶訓練”過程。
(4)網路趨向收斂即網路的總體誤差趨向極小值的“學習收斂”過程。
在訓練階段中,訓練實例重複通過網路,同時修正各個權值,改變連線權值的目的是最小化訓練集誤差率。繼續網路訓練直到滿足一個特定條件為止,終止條件可以使網路收斂到最小的誤差總數,可以是一個特定的時間標準,也可以是最大重複次數。
軟體實現
用C語言實現的BP算法步驟如下:
1)初始化,用小的隨機數給各權值和閾值賦初值。注意不能使網路中各初始權值和閾值完全相等,否則網路不可能從這樣的結構運行到一種非等權值結構。
2)讀取網路參數和訓練樣本集。
3)歸一化處理。
4)對訓練集中每一樣本進行計算。
①前向計算隱層、輸出層各神經元的輸出。
②計算期望輸出與網路輸出的誤差。
③反向計算修正網路權值和閾值。
5)若滿足精度要求或其他退出條件,則結束訓練,否則轉步驟4)繼續。
6)結果分析與輸出。
不足
雖然BP算法得到廣泛的套用,但它也存在不足,其主要表現在訓練過程不確定上,具體如下。
(1)訓練時間較長。對於某些特殊的問題,運行時間可能需要幾個小時甚至更長,這主要是因為學習率太小所致,可以採用自適應的學習率加以改進。
(2)完全不能訓練。訓練時由於權值調整過大使激活函式達到飽和,從而使網路權值的調節幾乎停滯。為避免這種情況,一是選取較小的初始權值,二是採用較小的學習率。
(3)易陷入局部極小值。BP算法可以使網路權值收斂到一個最終解,但它並不能保證所求為誤差超平面的全局最優解,也可能是一個局部極小值。這主要是因為BP算法所採用的是梯度下降法,訓練是從某一起始點開始沿誤差函式的斜面逐漸達到誤差的最小值,故不同的起始點可能導致不同的極小值產生,即得到不同的最優解。如果訓練結果未達到預定精度,常常採用多層網路和較多的神經元,以使訓練結果的精度進一步提高,但與此同時也增加了網路的複雜性與訓練時問。
(4)“喜新厭舊”。訓練過程中,學習新樣本時有遺忘舊樣本的趨勢。