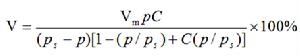兩個假定
1.BET方程是建立在Langmuir吸附理論基礎上的，但同時還認為：物理吸附為分子間力，被吸附的分子與氣相分子之間仍有此種力，故可發生多層吸附，多層吸附與氣體的凝聚相似。
2.吸附達到平衡時，每個吸附層上的蒸發速度等於凝聚速度，故能對每層寫出相應的吸附平衡式，經過一定的數學運算得到BET方程。
表達式
其表達式為：
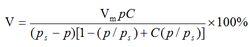BET方程（此等溫式被公認為測定固體表面積的標準方法）
V—平衡壓力為P時，吸附氣體的總體積。
Vm—催化劑表面覆蓋第一層滿時所需氣體的體積。
P—被吸附氣體在吸附溫度下平衡時的壓力。
Ps—飽和蒸汽壓力。
C—與被吸附有關的常數。
式中：V為吸附氣體的體積；Vm為單分子層吸附時的吸附量；p0為在吸附溫度下吸附質的飽和蒸汽壓；C為常數，與吸附質的汽化熱有關。根據在給定溫度下測得不同分壓p下某種氣體的吸附體積，由圖解法可求得C和Vm的值。若已知每個氣體分子在吸附劑表面所占的面積，就可求得吸附劑的表面積。這就是測定吸附劑和催化劑表面積的BET法。BET方程套用範圍較廣，適用於多孔材料（如：活性炭）的吸附。
BET方程測定常用的吸附質是N2、Ar、He等，其截面積可查。
由BET法可延伸得到B點法和一點法
