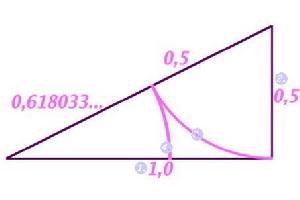
黃金分割率
 黃金分割實例
黃金分割實例1/0.618=1.618
(1-0.618)/0.618=0.618
這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建築等藝術領域,而且在管理、工程設計等方面也有著不可忽視的作用。
讓我們首先從一個數列開始,它的前面幾個數是:1、1、2、3、5、8、13、21、34、55、89、144…..這個數列的名字叫做"斐波那契數列",這些數被稱為"斐波那契數"。特點是即除前兩個數(數值為1)之外,每個數都是它前面兩個數之和。
斐波那契數列與黃金分割有什麼關係呢?經研究發現,相鄰兩個斐波那契數的比值是隨序號的增加而逐漸趨於黃金分割比的。即f(n-1)/f(n)-→0.618…。由於斐波那契數都是整數,兩個整數相除之商是有理數,所以只是逐漸逼近黃金分割比這個無理數。但是當我們繼續計算出後面更大的斐波那契數時,就會發現相鄰兩數之比確實是非常接近黃金分割比的。
一個很能說明問題的例子是五角星/正五邊形。五角星是非常美麗的,我們的國旗上就有五顆,還有不少國家的國旗也用五角星,這是為什麼?因為在五角星中可以找到的所有線段之間的長度關係都是符合黃金分割比的。正五邊形對角線連滿後出現的所有三角形,都是黃金分割三角形。
由於五角星的頂角是36度,這樣也可以得出黃金分割的數值為2Sin18。
黃金分割點
約等於0.618:1
是指分一線段為兩部分,使得原來線段的長跟較長的那部分的比為黃金分割的點。線段上有兩個這樣的點。
利用線段上的兩黃金分割點,可作出正五角星,正五邊形。
2000多年前,古希臘雅典學派的第三大算學家歐道克薩斯首先提出黃金分割。所謂黃金分割,指的是把長為L的線段分為兩部分,使其中一部分對於全部之比,等於另一部分對於該部分之比。而計算黃金分割最簡單的方法,是計算斐波契數列1,1,2,3,5,8,13,21,...後二數之比2/3,3/5,5/8,8/13,13/21,...近似值的。
黃金分割傳播
黃金分割在文藝復興前後,經過阿拉伯人傳入歐洲,受到了歐洲人的歡迎,他們稱之為"金法",17世紀歐洲的一位數學家,甚至稱它為"各種算法中最可寶貴的算法"。這種算法在印度稱之為"三率法"或"三數法則",也就是我們現在常說的比例方法。
其實有關"黃金分割",我國也有記載。雖然沒有古希臘的早,但它是我國古代數學家獨立創造的,後來傳入了印度。經考證。歐洲的比例算法是源於我國而經過印度由阿拉伯傳入歐洲的,而不是直接從古希臘傳入的。
因為它在造型藝術中具有美學價值,在工藝美術和日用品的長寬設計中,採用這一比值能夠引起人們的美感,在實際生活中的套用也非常廣泛,建築物中某些線段的比就科學採用了黃金分割,舞台上的報幕員並不是站在舞台的正中央,而是偏在台上一側,以站在舞台長度的黃金分割點的位置最美觀,聲音傳播的最好。就連植物界也有採用黃金分割的地方,如果從一棵嫩枝的頂端向下看,就會看到葉子是按照黃金分割的規律排列著的。在很多科學實驗中,選取方案常用一種0.618法,即優選法,它可以使我們合理地安排較少的試驗次數找到合理的西方和合適的工藝條件。正因為它在建築、文藝、工農業生產和科學實驗中有著廣泛而重要的套用,所以人們才珍貴地稱它為"黃金分割"。
黃金分割〔GoldenSection〕是一種數學上的比例關係。黃金分割具有嚴格的比例性、藝術性、和諧性,蘊藏著豐富的美學價值。套用時一般取0.618,就像圓周率在套用時取3.14一樣。
發現歷史
由於公元前6世紀古希臘的畢達哥拉斯學派研究過正五邊形和正十邊形的作圖,因此現代數學家們推斷當時畢達哥拉斯學派已經觸及甚至掌握了黃金分割。
公元前4世紀,古希臘數學家歐多克索斯第一個系統研究了這一問題,並建立起比例理論。
公元前300年前後歐幾里得撰寫《幾何原本》時吸收了歐多克索斯的研究成果,進一步系統論述了黃金分割,成為最早的有關黃金分割的論著。
中世紀後,黃金分割被披上神秘的外衣,義大利數家帕喬利稱中末比為神聖比例,並專門為此著書立說。德國天文學家克卜勒稱黃金分割為神聖分割。
到19世紀黃金分割這一名稱才逐漸通行。黃金分割數有許多有趣的性質,人類對它的實際套用也很廣泛。最著名的例子是優選學中的黃金分割法或0.618法,是由美國數學家基弗於1953年首先提出的,70年代在中國推廣。
黃金分割奇妙之處,在於其比例與其倒數是一樣的。例如:1.618的倒數是0.618,而1.618:1與1:0.618是一樣的。
確切值為(√5-1)/2
黃金分割
是古希臘哲學家畢達哥拉斯發現的。經過反覆比較,他最後確定1:0.618的比例最完美。後來,德國的美學家澤辛把這一比例稱為黃金比例。
推導方法
正五角形求法
做正五角形ABCDE(按順時針順序標),點A,點C之間連線,黃金分割率=直線AB/直線AC。
由(5-2)*180/5=108,求出每個角的度數。直線AB=BC,所以∠BAC和∠BCA都為(180-108)/2=36°
講直線AB朝B端延長一倍,端點設為F,連線CF,形成一個直角三角形(求證方法太複雜了,就不一一敘述了)。Cosine∠BAC=直線AC/AF=1/(2(直線AB)/AC)
1/(Cosine36)=2(直線AB/AC)
1/(2(Cosine36))=直線AB/AC=0.618...x,2x,√5
三角形求法
隨意取一個長度做直線AB,用它兩倍的長度做一個直角邊AC,在連線BC,可以用勾股定律算出斜邊的長度是根號五個AB的長度。
用方程解,此時的三角形就是一個x,2x,根號5x三角形。
在直線BC的B端向內截出一個x的長度,這裡就出現的黃金分割率,(根號5-1)/2=根號1.25/0.5=0.618...
用尺規做黃金分割的方法
已知線段AB,求AB的黃金分割點F
作法:
1、作AB的垂直平分線,垂足O,在其上取OC=AB
2、連AC,
3、在CA上截取CD=OA
4、在AB上截取AF=AD
F就是要作的點。
證明:
設AB=1,則AO=1/2,OC=1,CA=√5/2,CD=1/2
AF=AD=(√5-1)/2
F是AB的黃金分割點
具體數位
黃金分割數是無理數,前面的1024位
0.61803398874989484820458683436563811772030917980576
28621354486227052604628189024497072072041893911374
84754088075386891752126633862223536931793180060766
72635443338908659593958290563832266131992829026788
06752087668925017116962070322210432162695486262963
13614438149758701220340805887954454749246185695364
86444924104432077134494704956584678850987433944221
25448770664780915884607499887124007652170575179788
34166256249407589069704000281210427621771117778053
15317141011704666599146697987317613560067087480710
13179523689427521948435305678300228785699782977834
78458782289110976250030269615617002504643382437764
86102838312683303724292675263116533924731671112115
88186385133162038400522216579128667529465490681131
71599343235973494985090409476213222981017261070596
11645629909816290555208524790352406020172799747175
34277759277862561943208275051312181562855122248093
94712341451702237358057727861600868838295230459264
78780178899219902707769038953219681986151437803149
97411069260886742962267575605231727775203536139362
107673893764556060605922...