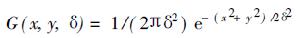簡介
在計算機視覺中， 高斯差分函式，即 高斯差（英語：Difference of Gaussians，簡稱“DOG”）是一種將一個原始灰度圖像的模糊圖像從另一幅灰度圖像進行增強的算法，通過DOG以降低模糊圖像的模糊度。這個模糊圖像是通過將原始灰度圖像經過帶有不同標準差的高斯核進行卷積得到的。用高斯核進行高斯模糊只能壓制高頻信息。從一幅圖像中減去另一幅可以保持在兩幅圖像中所保持的頻帶中含有的空間信息。這樣的話，DOG就相當於一個能夠去除除了那些在原始圖像中被保留下來的頻率之外的所有其他頻率信息的帶通濾波器。
數學原理
DOG是一個空總額的小波母函式，它從一個窄高斯減去一個寬高斯，是墨西哥帽小波的一個近似。一維情況下它的定義公式如下：
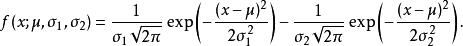高斯差分函式細節及套用
作為一個增強算法，DOG可以被用來增加邊緣和其他細節的可見性，大部分的邊緣銳化運算元使用增強高頻信號的方法，但是因為隨機噪聲也是高頻信號，很多銳化運算元也增強了噪聲。DOG算法去除的高頻信號中通常包含了隨機噪聲，所以這種方法是最適合處理那些有高頻噪聲的圖像。這個算法的一個主要缺點就是在調整圖像對比度的過程中信息量會減少。
當它被用於圖像增強時，DOG算法中兩個高斯核的半徑之比通常為4:1或5:1。當設為1.6時，即為高斯拉普拉斯運算元的近似。高斯拉普拉斯運算元在多尺度多解析度像片。用於近似高斯拉普拉斯運算元兩個高斯核的確切大小決定了兩個高斯模糊後的影像間的尺度。
DOG也被用於尺度不變特徵變換中的斑點檢測。事實上，DOG算法作為兩個多元常態分配的差通常總額為零，把它和一個恆定信號進行卷積沒有意義。當K約等於1.6時它很好的近似了高斯拉普拉斯變換，當K約等於5時又很好的近似了視網膜上神經節細胞的視野。它可以很好的作為一個實時斑點檢測運算元和尺度選擇運算元套用於遞歸程式。
更多信息
在DOG算法中，它被認為是在模擬視網膜上的神經從影像中提取信息從而提供給大腦。
其他
•馬爾-希爾德雷斯算法
•斑點檢測中的DOG算法
•斑點檢測
•尺度空間
•尺度不變特徵變換
