馮·諾依曼期望效用函式

P1u(x1) P2u(x2) )其中，E表示關於隨機變數X的期望效用。

即VNM效用函式。
不過, 該理論是將個體和群體合而為一的。後來，阿羅和德布魯（Arrow and Debreu）將其吸收進瓦爾拉斯均衡的框架中，成為處理不確定性決策問題的分析範式，進而構築起現代個體經濟學並由此展開的包括巨觀、

金融、計量等在內的宏偉而又優美的理論大廈。
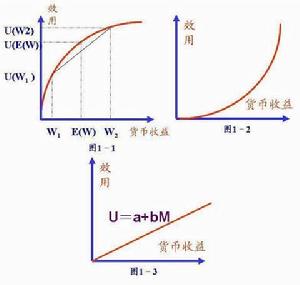
如果某個隨機變數X以機率Pi取值xi，i=1,2,…,n，而某人在確定地得到xi時的效用為u(xi)，那么，該隨機變數給他的效用便是：
U(X) = E = P1u(x1) + P2u(x2) + ... + Pnu(xn)
其中，E表示關於隨機變數X的期望效用。因此U(X)稱為期望效用函式，又叫做馮·諾依曼—摩根斯坦效用函式（VNM函式）。另外，要說明的是期望效用函式失去了保序性，不具有序數性。