馬哈維拉(Mahāvīra)
9世紀活躍於印度邁索爾.數學.
 馬哈維拉
馬哈維拉馬哈維拉的工作屬於純數學領域,對天文學問題幾乎沒有涉獵.這與他的前輩們是頗為不同的.在古代印度,數學家一般也是天文學家.
馬哈維拉的《計算精華》
共含9章:(1)術語;(2)算術運算;(3)與分數有關的運算;(4)有各種特點的運算;(5)與三分律(比例律)有關的運算;(6)混合運算;(7)面積計算;(8)與挖掘有關的計算;(9)與影子有關的計算.
馬哈維拉改進和推廣了他的前輩們的許多結果,其中最有特色的研究包括:零的運算、二次方程、利率計算、整數性質、排列組合、單分數法則,等等.
1.零的算法
《計算精華》中敘述了零的算法:“一個數乘零得零,一個數加零、減零或除以零,這數都不變”.這表明,當時尚未認識到零不能作除數.
 計算
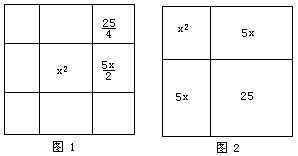
計算2.一元二次方程和不定方程
在這方面,成書於約公元1世紀時的中國《九章算術》已有較多的成果.公元3世紀時,希臘數學家丟番圖(Diophantus)著《算術》一書,也解決了不少二次方程、不定方程問題,但他不承認負數的合理性.馬哈維拉以前的印度數學家不斷地研究了這些方程的解法,阿耶波多(Aryabhata I)建立了求一次線性不定方程正整數通解的法則,即庫塔卡(Kuttaka).婆羅摩笈多(Brahmagupta)給出了一元二次方程的一個求根公式.馬哈維拉也討論了很多這方面的問題.
馬哈維拉對庫塔卡也作了一些改進.他在倒回去求方程的解時省略了用第一個商數參與運算的一步,一個未知數是用代入方程法求得的.但他總是躲閃著不讓輾轉除法的餘數為0,這其實是不必要的.
3.“花環數”
兩整數相乘,若其乘積的數字呈中心對稱,馬哈維拉便稱之為“花環數”,例如:
14287143×7=100010001;
142857143×7=1000000001;
12345679×9=111111111;
333333666667×33=11000011000011;
11011011×91=1002002001;
27994681×441=12345654321.
他對這種狀似花環的特殊整數的構成規律進行了研究.
4.排列組合
古代耆那教典籍中含有一些簡單的排列組合問題,馬哈維拉給出公式
在幾何學方面,馬哈維拉重新研究了婆羅摩笈多關於邊為有理數的圓內接四邊形的作圖.像婆羅摩笈多一樣,馬哈維拉也沒有覺察到這類四邊形必須是內接於圓的.
馬哈維拉所討論過的幾何作圖問題很多,例如:(1)給定一條邊,作一個其他兩邊均為有理數的直角三角形;(2)給定一斜邊c求作一直角三角形,使二直角邊均為有理數;(3)求作一個三邊相等的梯形;(4)求作一有給定面積的圓內接四邊形;(5)作一有給定周長的圓內接四邊形;(6)求作一長方形,使其面積在數量上是其周長或對角線長的倍數,或者一般地,是其邊長與對角線長的線性組合;
