餘割函式

餘割函式就是對於任意一個實數x，都對應著唯一的角（弧度制中等於這個實數），而這個角又對應著唯一確定的餘割值cscx與它對應，按照這個對應法則建立的函式稱為餘割函式。一個角的頂點和該角終邊上另一個任意點之間的距離除以後一個點的非零縱坐標所得之商，這個角的頂點與平面直角坐標系的原點重合，而其始邊則與正X軸重合。記作cscx.它與正弦的比值表達式互為倒數。餘割的函式圖像為奇函式，且為周期函式。餘割函式記為：y=cscα。餘割函式最小正周期為2π。

基本信息

• 中文名：餘割函式

• 定義域：{x|x≠kπ，k∈Z}
• 值域：{y|y≤-1或y≥1}
• 奇偶性：奇函式
• 周期性：最小正周期為2π

餘割函式的定義

對於任意一個實數x，都對應著唯一的角（弧度制中等於這個實數），而這個角又對應著唯一確定的餘割值cscx與它對應，按照這個對應法則建立的函式稱為餘割函式。
記作f(x)=cscx

餘割函式的性質

1、定義域：{x|x≠kπ，k∈Z}
2、值域：{y|y≤-1或y≥1}
3、奇偶性：奇函式
4、周期性：最小正周期為2π
5、圖像：
圖像漸近線為：x=kπ ，k∈Z 餘割函式與正弦函式互為倒數

其他

1、在三角函式定義中，cscα=r/y
2、餘割與正弦互為倒數

圖像

函式圖象：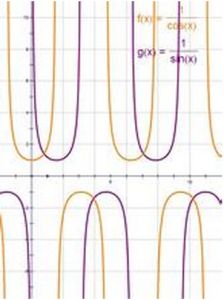

餘割函式