簡介
信號分析原理測試信號的頻域分析是把信號的幅值、相位或能量變換以頻率坐標軸表示,進而分析其頻率特性的一種分析方法又稱為頻譜分析。對信號進行頻譜分析可以獲得更多有用信息,如求得動態信號中的各個頻率成分和頻率分布範圍,求出各個頻率成分的幅值分布和能量分布,從而得到主要幅度和能量分布的頻率值。
套用
由時間函式求頻譜函式的傅立葉變換公式就是將該時間函式乘以以頻率為係數的指數函式之後,在從負無限大到正無限大的整個區間內,對時間進行積分,這樣就得到了與這個時間函式對應的,以頻率為自變數的頻譜函式。頻譜函式是信號的頻域表示方式。根據上述傅立葉變換公式,可以求出常數(直流信號)的頻譜函式為頻域中位於零頻率處的一個衝激函式,表示直流信號就是一個頻率等於零的信號。與此相反,衝激函式的頻譜函式等於常數,表示衝激函式含有無限多個、頻率無限密集的正弦成分。同樣的,單個正弦波的頻譜函式就是頻域中位於該正弦波頻率處的一對衝激函式。
利用傅立葉變換的方法對振動的信號進行分解,並按頻率順序展開,使其成為頻率的函式,進而在頻率域中對信號進行研究和處理的一種過程,稱為頻譜分析。
目的
將信號在時間域中的波形轉變為頻率域的頻譜,進而可以對信號的信息作定量解釋。
套用軟體
對信號進行頻譜分析,是對其進行傅立葉變換,得到其振幅譜與相位譜。分析軟體主要為Matlab。
對於信號來說,分模擬信號與數位訊號。進行頻譜分析時,對於模擬信號來說,首先對其進行抽樣,使其離散化,然後利用離散傅立葉變換(DFT)或者快速傅立葉變換(FFT),然後對其幅度(ABS)和相位(ANGLE)的圖像進行分析,而對於數位訊號來說,則可直接進行離散傅立葉變換或快速傅立葉變換。
主要課程
電子信息、通信方向、地震資料處理的課程,如信號與系統,隨機信號分析,數位訊號處理等
工具
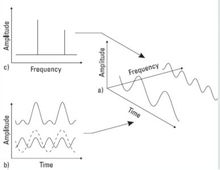 頻譜分析
頻譜分析頻譜分析儀等工具可較為方便的觀察其頻譜。
就量測信號的技術觀之,時域方面,示波器為一項極為重要且有效的量測儀器,它能直接顯示信號波幅、頻率、周期、波形與相位之回響變化,目前,一般的示波器至少為雙軌跡輸出顯示裝置,同時也具有與繪圖儀連線的IEEE-488、IEEE-1394 或RS-232 接口功能,能將螢幕上量測顯示的信息繪出,作為研究比較的依據,但它僅局限於低頻的信號,高頻信號則有其實際的困難。頻譜分析儀乃能彌補此項缺失,同時將一含有許多頻率的信號用頻域方式來呈現,以識別在各個頻率的功率裝置,以顯示信號在頻域裡的特性。圖1.說明方波在時域與頻域的關係,此立體坐標軸分別代表時間、頻率與振幅。由傅立葉級數(Fourier Series)可知方波包含有基本波(Fundamental Wave)及若干諧波(Harmonics),信號的組合成份由此立體坐標中對應顯示出來。低頻時,雙軌跡模擬與數字示波器為目前信號時域的主要量測設備,模擬示波器可量測的輸入信號頻率可達100 MHz,數字示波器有100 MHz 與400(或500)MHz 等多種。螢幕上顯示信號的意義為橫軸代表時間,縱軸代表信號電壓的振幅,用示波器量測可得到信號時間的相位及信號與時間的關係,但無法獲知信號失真的數據,亦即無法獲知信號諧波分量的分布情況,同時量測微波領域(如UHF 以上的頻帶)信號時,基於設備電子組件功能的限制、輸入端雜散電容等因素,量測的結果無可避免地將產生信號失真及衰減,為解決量測高頻信號上述的問題,頻譜分析儀為一適當而必備的量測儀器,頻譜分析儀的主要功能是量測信號的頻率回響,橫軸代表頻率,縱軸代表信號功率或電壓的數值,可用線性或對數刻度顯示量測的結果。
另外它的信號追蹤產生器(Tracking Generator)可直接量測待測件DUT(Device Under Test)的頻率回響特性,但它只能量測振幅無法量測相位。就高頻信號領域觀之,頻譜分析儀是電子工程技術人員不可或缺的設備,對頻譜分析儀工作原理的了解將有助於信號量測系統的建立及充分擴展其套用範疇。
頻譜分析儀的套用領域相當廣泛,諸如衛星接收系統、無線電通信系統、行動電話系統基地台輻射場強的量測、電磁干擾等高頻信號的偵測與分析,同時也是研究信號成份、信號失真度、信號衰減量、電子組件增益等特性的主要儀器。
仿真實例
信號的頻譜分析
a=10; %波信號振幅
fb1=3e6; %頻率fb1
fb2=4e6; %頻率fb2
fs=2.4*fb2; %抽樣頻率fs
T=1e-5; %調頻周期,也可設定抽樣點數
t=0:(1/fs):(T-1/fs);
N=length(t);
df=fs/N;
f=0:df:(N-1)*fs/N;
x=1/fs*a*(cos(2*pi*fb1.*t)+cos(2*pi*fb2.*t)); %線性調頻連續波信號
subplot(4,1,1);
plot(t,x);
title('波信號')
subplot(4,1,2);
stem(t,x);
title('抽樣後');
subplot(4,1,3);
stem(f,abs(fft(x,N)));
title('頻譜幅度');
subplot(4,1,4);
stem(f,angle(fft(x,N)));
title('頻譜相位');