聲譜分析
正文
對聲波或振動進行計算或測量,以取得關於它們的組成和能量的頻率分布圖形的技術及工作的統稱。研究表明,振動系統的結構特點、振動方式和聲譜的形態之間存在著明顯的對應關係,如周期性振動的聲譜為線譜,它可以分解成許多個與基頻成整倍數關係的簡諧振動;撞擊引起的阻尼振動的聲譜則為連續譜;樂器發出的聲音的頻譜不僅反映曲調,而且反映樂器的品種;語言的聲譜對經過訓練的人或具備記憶、對比和按邏輯條件作出判斷功能的機器來說,都是"可讀的",根據聲譜可以辨意和識別說話人。
聲譜分析在現代人的生活中發揮著重大作用:對噪聲污染的控制可通過聲譜分析,了解噪聲源特點後有效地採取針對性消聲和減振措施;工業生產中機械的安裝、調整和運轉可藉助聲譜分析進行監察。聲譜分析在樂器製作工藝的科學檢驗、通信和廣播設備的有效利用方面都有廣泛的套用。譬如說,為了使電話能夠在通頻頻寬只有大約 100Hz的連線美歐兩洲的海底電纜中傳輸而發展起來的,自20世紀60年代以來,在軍事通信部門廣泛套用的通道式聲碼器的使用,就需要不斷地傳送通話的聲譜數據;目前正處於積極研製過程中的人機對話語言自動翻譯機,其語言識別和語言合成(見語言聲學)部分更是離不開聲譜分析手段和對語言聲譜知識的了解;在人身保健方面、心音、腸鳴等過去全憑醫生聽覺感受和經驗來診斷的生理-物理現象,近年來,隨著聲譜分析技術的普及也開始利用它來幫助診斷;在海防線上,對於敵方潛艇的侵犯要進行的檢測和識別,也依靠廣泛的聲譜分析。
聲譜的計算 1822年法國數學家J.B.J.傅立葉提出了一個重要概念,就是說,任何函式,尤其是周期函式,都可以表達為基本的三角函式之和,用數學表達式寫出來就是
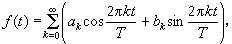 (1)
(1)
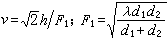 (2)
(2)
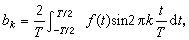 (3)
(3)
實際的聲或振動是有起止點的。尤其是因為任何聲或振動過程只能在一有限期間受到觀察和分析;在計算聲譜時,這一期間被當作是相應傅立葉函式的周期T。此外,對被觀察和分析過程的抽樣取值總在離散的特定時刻進行,根據"上限頻率為F的連續函式可由相距為1/2F的各個時刻的取樣值在函式存在期間單一地代表"這一抽樣定理,抽樣率一般選定為等於或略大於上限頻率的二倍。這樣,對於具體的聲或振動過程,只要上限頻率已知,按照間隔為1/2F的抽樣率取值可以得到t=n/2F(n=0,1,2,...,N-1)各點的函式值fn(t),在離散時間情況下用求和代替積分就可以把公式(2)及(3)改寫成便於用數字計算機進行幅度譜及相位譜數值計算的離散傅立葉變換(DFT)。
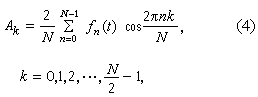
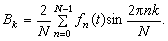 (5)
(5)
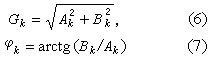
對於實際存在的聲過程來說,即使給出了f(t)的記錄,根據傅立葉變換算出Ak、Bk並得出聲譜來的計算非常煩瑣和費時。在60年代初期快速傅立葉變換 (FFT)尚未提出,儘管當時已有每秒能作上萬次運算的電子計算機可用,但運算還很費時,輸入聲過程的數據,編製程序等都有一些麻煩要克服,人們仍然不能通過傅立葉變換來考察實際振動或聲波的頻譜。進入70年代後,由於利用公因子提出以減少乘法運算次數,常用數值可存儲查表等的快速傅立葉變換問世,廉價的功能強大的小型和微型計算機的成批生產,聲過程輸入計算機和頻譜分析結果的顯示技術手段都已達到便於使用的地步,按照傅立葉變換計算頻譜的方法已經成熟,專用的FFT器件和包括換能器、傅立葉變換裝置、聲譜顯示、記錄和繪圖設施的成套頻譜測量分析儀紛紛問世,並成為新時代頻譜分析的重要手段。
濾波測量 把聲或振動信號用傳聲器或拾振器轉換為電信號,通過具有頻率選擇性的濾波器系統以分離頻率分量並測量其聲壓級或振動的位移、速度、加速度是頻譜分析方法的另一個重要方面。從20世紀20年代到快速傅立葉變換算法付諸實用之前的這段時期,濾波測量是頻譜分析的主要手段。
由於頻譜測量採取了先把聲或振動信號轉換成電信號,然後對電信號濾波,測量其大小並加以記錄的辦法,濾波測量技術的演變是伴隨著電子技術的發展進行的。 20年代到 60年代主要用電感和電容組合的無源濾波器;60年代到70年代盛行的是電阻和電容加電晶體放大器或集成塊運算放大器構成的有源濾波器。70年代以後隨著電信號的處理由連續轉向離散為主,出現了數字濾波器、開關電容濾波器等單片集成塊。在80年代初已經製成了用16個帶通開關電容濾波器組覆蓋最重要的可聽聲頻帶,動態範圍大於43dB,頻率準確度高於1%,包括能量檢測部分的單片頻率分析器件。
由無源濾波器和電子管為核心作成的頻譜分析設備體積大而笨重。為了縮小這類測試儀器的尺寸,減輕重量,人們曾經提出過只用一隻固定通頻帶的濾波器,而寬頻帶的覆蓋任務用外差方法產生拍頻效應來完成,另外,對頻譜分析結果不採取多道記錄,而是用單道通過快速掃描來實現順序記錄。
有源濾波器的聲譜測量設備的體積和重量較之無源濾波器的相同功能設備已經縮小和減輕很多,但是一般適宜在實驗室條件下使用,從在各種條件下使用都很方便的要求衡量,單片頻譜分析器件算是能滿足低成本、低功耗、體積小、重量輕、性能好而穩定的新時代產品。
數字濾波器,利用狀態延時和疊加來產生波的干涉效應,達到分離不同頻率分量的目的。為了實現對時間上連續變化的電(聲)信號x(t)進行濾波,首先要對它按照頻率範圍進行適當的定時抽樣以得到離散序列x(0),x(T),x(2T),...,x(kT), 然後使此離散過程經過各種延時,再按照一定的組合關係給以計數和疊加,這樣得到的新過程
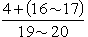 (8)
(8)
聲譜分析的一些實際問題及其解決途徑 ①選定適當的分析期間。實際生活中的聲或振動現象除了可由確定性的參量制約,因而可以用任何一次觀測對其作準確的定量描述的確定性過程外,還有因生產、傳播和接收系統的參量有偶然性起伏,只能根據大量採樣用統計語言描述的隨機過程。對隨機過程的觀察要用較長的觀察分析時間或者要進行多次觀察以便用經過積累及平均使穩定的必然性因果關係的比重增加,保存下來而偶然性的影響由於存在相互抵消的可能性而最終大大地減小。②用方便的方法判定所考察過程的屬性。人們對所考察的過程的屬性往往存在疑問,經常出現檢驗兩個過程相似性的要求。為此人們很自然地想到移動時間軸使兩個時間函式儘可能地重合的辦法和從相應的頻譜數據在頻率取樣點一致情況下看看它們的振幅或能量分布是否存在差異和差距大小的辦法。相關函式判斷準則的出現和套用,是從時間域觀點進行檢驗的必然結果,而在計算兩幀頻譜差異的時候,必然要形成和套用互譜,作為相似性判斷準則。
參考書目
戈爾德、雷道等著,高哲民等譯:《訊號的數字處理》,地質出版社,北京,1980。(B. Gold and C. M.Radar,Digtal Processing of Signals, McGraw-Hill, New York,1969.)
C. H. Chen, Digtal Wave from Processing and Recognition,CRC Press,Boca Raton,Florida,1963.