失真的分類及原因
失真產生的原因
運算放大器廣泛套用在各種電路中,不僅可以實現加法和乘法等線性運算電路功能,而且還能構成限幅電路和函式發生電路等非線性電路,不同的連線方式就能實現不同的電路功能。集成運放將運算放大器和一些外圍電路集成在一塊矽片上,組合成了具有特定功能的電子電路。集成運放體積小,使用方便靈活,適合套用在移動通信和數碼產品等便攜設備中。
但在實際工程套用中,由於種種原因,總是會出現輸入波形不能正常放大,這就是放大電路的失真現象。失真現象主要有兩大種類型:線性失真和非線性失真。造成線性失真的主要原因是放大器的頻率特性不夠好。而造成非線性失真的原因有電晶體等特性的非線性和靜態工作點位置設定的不合適或輸入信號過大。
非線性失真
非線性失真亦稱波形失真、非線性畸變,表現為系統輸出信號與輸入信號不成線性關係,它與線性失真的本質差別是由電子元器件的非線性所引起,使輸出信號中產生新的諧波成分,改變了原信號頻譜。造成非線性失真的原因主要有電晶體等特性的非線性和靜態工作點位置設定的不合適或輸入信號過大。由於放大器件工作在非線性區而產生的非線性失真有一下幾種:飽和失真、截止失真、雙向失真、交越失真、諧波失真、互調失真、不對稱失真、瞬態互調失真。
頻率失真的原因
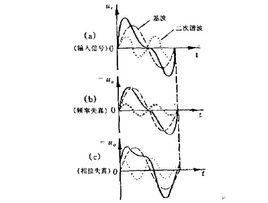
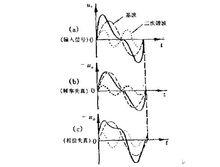 複雜信號的失真波形
複雜信號的失真波形在放大電路的輸入信號是多頻信號時,如果放大電路對信號的不同頻率分量具有不同的增益幅值,就會導致輸出波形發生失真,稱為幅度失真;如果相對相移發生變化,稱為相位失真,這兩者統稱為頻率失真。頻率失真是由電路的線性電抗元件引起的,頻率失真的特徵是輸出信號中不產生輸入信號中所沒有的新的頻率分量。如右圖,為輸入多頻複雜信號時經過放大電路後產生相位失真和幅度失真的信號波形。造成線性失真的原因主要是放大器的頻率特性不夠好。
頻率失真的類型
根據上述原因,頻率失真可分為幅度失真和相位失真。
幅度失真
由傅立葉分析的基本理論,任何一周期信號都可以分解為直流分量,基波分量和各次諧波分量的加權。而諧波就是頻率為基波整數倍的餘弦信號。若為基波的N倍,即稱為N次諧波。可見,如果一個系統對不同頻率分量的放大倍數不同,那么對不同的諧波分量將有不同的放大倍數。當一個信號通過系統之後,各諧波分量的幅度發生了改變,加權後將不能真實反應原信號。
相位失真
從相位的角度來考慮,如果原信號的各次諧波通過這個系統,產生了不同的相移(表現為時域為不同的延遲),則系統輸出的各次諧波加權之後,也不能真實反應原信號。
改善頻率失真的方法
在我們日常生活中,語言、圖像、音樂等信號都是由基波分量和諧波分量疊加而成的複雜信號,如對於一部電話機、頻率失真很小時,從電話中雙方還能相互分清;失真嚴重時甚至無法辨清對方性別,又如對電視圖像信號來說,若視頻放大器產生高頻失真將使圖像細節不清晰;低頻失真時則造成背景亮度不均勻。對器樂合奏來說,當擴音器產生高頻失真將使樂音失去原有特色,給人以單調乏味的感覺,甚至無法聽;低頻失真則使渾厚雄壯的樂曲變得輕浮無力,這是因為基波分量決定音調和諧波分量決定音色的緣故為了減小頻率失真,使輸入信號中的高低頻分量均獲得與中頻同樣的增益,必須展寬放大器的通頻帶,使信號中的高低頻分量都處在通頻帶範圍內。
放大器的實際輸入信號通常是由許多頻率分量按照一定的幅度比例關係和相位關係疊加而成的非正弦信號。在放大器中由於器件的電抗效應和電抗性元件的存在,使得放大器對不同頻率信號具有不同的放大能力,即放大器的增益隨頻率不同而改變。影響低頻增益的主要因素是耦合電容和旁路電容,影響高頻增益的主要是結電容和引線等的雜散電容。為了減小這些因素帶來的頻率失真,使輸入信號中的高低頻分量均獲得與中頻同樣的增益,必須展寬放大器的通頻帶,使其在工作頻率內(如音頻為20HZ-20KHZ)近似滿足無失真傳輸條件。
常用的展寬通頻帶的方法有三種:補償電路法、負反饋法、組合電路法。
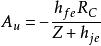 頻率失真
頻率失真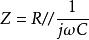 頻率失真
頻率失真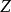 頻率失真
頻率失真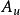 頻率失真
頻率失真(1)補償電路法:補償電路法如右圖中圖1。,。輸入高頻時,減小,增大,頻帶得到適當展寬。
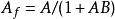 頻率失真
頻率失真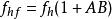 頻率失真
頻率失真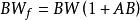 頻率失真
頻率失真(2)負反饋法:在加入負反饋後,如右圖中圖2所示。,,。可以看出,加入負反饋後,增益下降,但是頻帶卻得到了展寬。
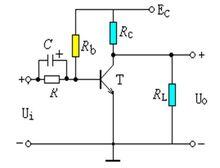 改善頻率失真的方法
改善頻率失真的方法(3)組合電路法:通過不同組態電路組合,改變電路的時間常數,提高高頻截頻。常用的有低阻輸入的共射-共基電路和低阻輸出的共集-共射電路,這幾種組合電路均可以提高截頻。
但是在實際工程研究和套用中,受電晶體特性等影響,通頻帶是不能無限展寬的,而且在展寬通頻帶的同時,會帶來其它弊端,尤其是會引入噪聲。所以不同的放大器,可以選擇不同的展寬頻帶方法,頻頻寬度可以視要求而定。