項名達(1789～1850)
正文
中國清代數學家，原名萬準，字步萊，號梅侶，浙江錢塘（今杭州市）人，祖籍安徽歙縣。生於乾隆五十四年,卒於道光三十年。嘉慶二十一年(1816)為舉人,考授國子監學正，道光六年(1826)成進士，改任知縣，但未就職。應考進士期間,曾在京盤桓數年,與友人研討數學，後返居故里。道光十七年(1837)前，主講苕南。此後，在杭州著名的三大書院之一紫陽書院執教，並研究數學。道光二十六年(1846)冬，退職還家，集中精力撰著書稿，主要數學著作有《象數一原》6卷(1849),《勾股六術》1卷(1825)，《三角和較術》1卷(1843)，《開諸乘方捷術》1卷(1845),後三種合刻為《下學庵算術》印行。《象數一原》的主要內容是論述三角函式冪級數展開式問題，他撰寫此書時已年老病重，僅寫成整分起度弦矢率論、半分起度弦矢率論、零分起度弦矢率論（兩卷）、諸術通詮、諸術明變,共6卷。其中卷四和卷六未能完稿，由其友人戴煦遵從他的囑託於鹹豐七年(1857)補寫完成，並為橢圓求周術補作圖解1卷,故現傳本《象數一原》共 7卷。在此書中，他推廣了明安圖和董祐誠(1791～1823)的結果。董祐誠同明安圖一樣，也用連比例的方法討論了全弧與分弧所對的弦的關係以及全弧和分弧的中矢（即該弧所張的弓形的高），得到四個冪級數公式。項名達進一步歸納為下列兩個公式:設сn和сm分別為圓內某弧с的n倍和m倍弧長，vn和vm分別為相應的中矢，r為圓半徑，則有
項名達的另一項成就是求出橢圓周長公式：
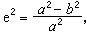α與b為橢圓長半軸與短半軸。這是中國在二次曲線研究方面最早的重要成果。他還據此推出圓周率倒數公式：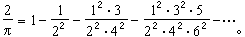 
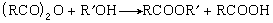近似值。《勾股六術》與《三角和較術》內容淺顯易懂，是項名達為初學者撰寫的數學入門書。在這兩卷書中,對於勾股形、平面三角形及球面三角形的各邊及其和、差的互求關係，做了較系統的分類與總結。