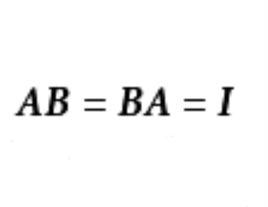基本介紹
先引進逆矩陣的概念。
對給定的矩陣 A，如果存在矩陣 B，使成立
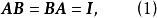非退化矩陣則稱 A為 非退化(矩)陣(non-degenerate matrix)，並稱適合式(1)的矩陣 B為 A的 逆(矩)陣(inverse matrix)；非退化陣也稱 可逆陣(invertible matrix)或 非奇異陣(non-singular matrix)。
可以看出，只有方陣才可能有逆矩陣，而且可以證明，對方陣 A， B，若 AB= I，則必 BA= I，故今後在討論方陣時，只要成立 AB= I或 BA= I就可以說明 A， B互為逆陣了 。
相關結論
定理 如果 A是非退化陣，則其逆陣是惟一的。
非退化矩陣
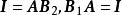非退化矩陣
非退化矩陣證： 可用同一法證明結論。設是對非退化陣 A的適合式(1)的任意兩個矩陣，則必有。事實上，根據以及下文式(2)，有
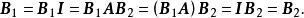非退化矩陣證畢。
在證明過程中巧用式(2)以及式(1)的做法，稱之為 單位陣技巧，這是在證明矩陣等式中時常有用的一種技巧，
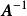非退化矩陣由於可逆陣 A的逆陣為惟一確定，故可記之為，有
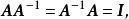非退化矩陣而稱不存在逆陣的方陣為 退化(矩)陣(degenerate matrix) 。
這樣，由逆陣概念可容易地推知，單位陣必為非退化陣，且其逆陣即為自身，即有
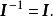非退化矩陣定理 對m×n矩陣 A，有
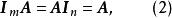非退化矩陣以及對適當維的零矩陣，總有
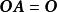非退化矩陣
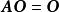非退化矩陣及 .
在有可能用上這些明顯等式時，能簡化矩陣乘法的運算過程。
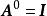非退化矩陣由於矩陣乘法是滿足結合律的，在一個方陣自乘若干次的情形，使用冪指數的記號是既合理又可帶來便利的。若k是個自然數，定義(規定)
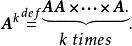非退化矩陣從這個定義可以看出成立 指數律：
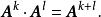非退化矩陣結論 一個n×n矩陣是非退化的充要條件是它的秩等於n。
推論 設 A， B都是數域F上的n×n矩陣，矩陣 AB為退化的充要條件是 A， B中至少有一個是退化的。
非退化矩陣
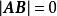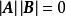非退化矩陣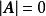 非退化矩陣
非退化矩陣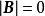 非退化矩陣
非退化矩陣
非退化矩陣 非退化矩陣證明 AB為退化學或 A退化或 B退化 。
