辛矩陣

概述

辛算法對於拋物型和雙曲型偏微分方程有著廣闊的套用前景[1-2].然而辛空間、辛變換及其相應的辛矩陣等是辛計算的基礎，數學,一個辛矢量空間是帶有辛形式ω的向量空間 V,所謂辛形式即一個非退化斜，辛矩陣表示空間的一個辛變換。取定一組基，ω 能表示為一個矩陣。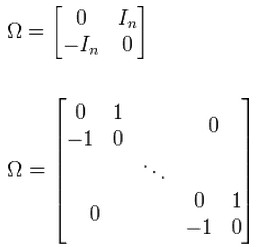

以上兩個條件表明這個矩陣必須是斜對稱非奇異矩陣。這不同於下面將介紹的辛矩陣，辛矩陣表示空間的一個辛變換。如果 V 是有限維的那么維數必須為偶數，因為每個奇數階斜對稱矩陣的行列式為 0。
非退化斜對稱雙線性形式和非退化“對稱”雙線性形式，比如歐幾里得向量空間的內積，的表現非常不同。歐幾里得內積 g，對任何非零向量 v，均有 g(v,v) > 0 成立；但是一個辛形式 ω 滿足 ω(v,v) = 0 。

辛矩陣的行列式等於1

一個2nX2n的矩陣 M（通常布於實數或複數域上）和A，使之滿足M‘AM=A,其中M'表 M的轉置矩陣,而 A是一個固定的可逆斜對稱矩陣即A=[0 E;-E 0].其中E是nXn階單位方陣，M的行列式等於一。