一般定義
定義1.1 設V是域P上的線性空間，σ∈Hom(V，V)，若存在λ∈Hom(V，V)，使λσ=E(單位線性變換)，則稱σ為 非奇異線性變換；否則，稱為奇異線性變換。
註：當dim V=n時，非奇異線性變換亦稱為非退化線性變換，或滿秩線性變換，或正則線性變換。在dim V=n的條件下，σ是可逆的充分必要條件為σ是非奇異的，因此，在有限維的條件下也可以說非奇異線性變換就是可逆線性變換。
線性代數中的定義
定義1.2 設x，x，...，x；y，y，...，y是兩組文字，係數在數域P中的一組關係式：
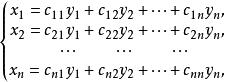非奇異線性變換稱為由x，x，...，x到y，y，...，y的一個 線性替換，或簡稱 線性替換。如果係數行列式
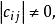非奇異線性變換那么上述線性替換就稱為非退化的。
例如 ，在解析幾何中，我們看到，當坐標原點與中心重合，一個有心二次曲線的一般方程是
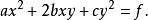非奇異線性變換為了便於研究這個二次曲線的幾何性質，我們可以選擇適當的角度θ，作轉軸（反時針方向轉軸）
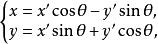非奇異線性變換
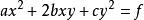非奇異線性變換把方程 化成標準方程。
如果把
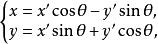非奇異線性變換看成線性替換，那么它就是非退化的，因為
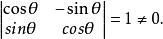非奇異線性變換性質
1. 因為二次型和它的矩陣是相互唯一決定的，令
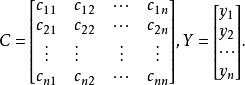非奇異線性變換故線性替換
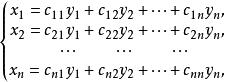非奇異線性變換可以寫成
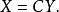非奇異線性變換2. 經過一個非退化的線性替換，二次型還是變成二次型。具體地：設
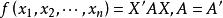非奇異線性變換是一個二次型，作非退化線性替換
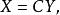非奇異線性變換
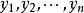非奇異線性變換我們可以得到一個的二次型
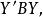非奇異線性變換故有
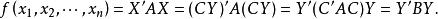非奇異線性變換容易看出，矩陣
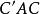非奇異線性變換也是對稱的，這就是前後兩個二次型的關係。
3. 經過非退化的線性替換，新二次型的矩陣與原二次型的矩陣是契約的。
