背景
預測控制算法最初是對線性系統提出的。當對象存在弱非線性時，採用這種線性預測控制算法也是十分有效的，因為弱非線性可視為一種模型失配，其影響可通過系統的魯棒性設計加以克服；必要時，還可通過線上辨識和自校正策略修改模型和控制律，以適應因弱非線性而引起對象特徵的變化。但是幾乎所有的實際控制系統都是非線性的，尤其是在實際的工業生產過程中，涉及的對象往往都是多輸入多輸出的複雜系統，具有很強的非線性，由於採用線性模型進行預測輸出與實際偏離較大，達不到最佳化控制的目的，模型線性化這一方法顯然不適用，因而必須基於非線性模型進行預測和最佳化。因此，提出了非線性模型預測控制方法。
預測控制
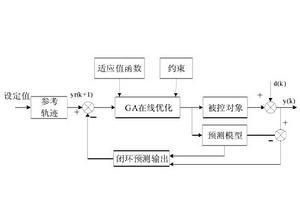
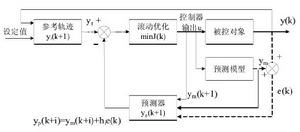圖 1 預測控制基本結構圖各類模型預測控制(MPC)算法雖然在模型、控制和 性能上存在許多差異， 但其核心都是在每個採樣周期，以系統當前狀態為起點，線上求解有限時域開環最優問題，得到一個最優控制序列，並將該序列的第一個控制量作用於被控系統，作為一種有限時域滾動最佳化策略，MPC 具有三個基本要素：預測模型、滾動最佳化和反饋校正。這一算法的基本結構如圖 1 所示，其基本原理圖如 2 所示。
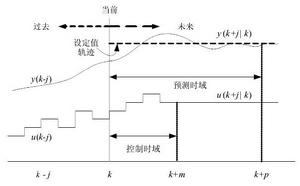圖 2 預測控制的基本原理
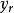非線性模型預測控制
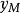非線性模型預測控制圖中，y 是系統當前輸出， 是根據設定值 w 和 y 求得的參考軌跡，
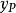非線性模型預測控制 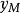非線性模型預測控制是預測模型的直接輸出， 是經反饋校正後的預測輸出，虛線部分 將與 y 之間的偏差 e 反饋給預測器以便進行反饋校正。各部分的功能如下：
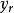非線性模型預測控制參考軌跡：它對改善閉環系統的動態特性及魯棒性起重要作用，根據 y 和設定值生成的 是從系統當前輸出到設定值的一條光滑軌跡。
滾動最佳化：在每個採樣周期，求解有限時域最佳化問題，並將求出的最優控制序列中對應當前時刻的部分套用於被控對象。
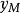非線性模型預測控制 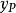非線性模型預測控制預測模型和預測器：基於模型和系統信息求出預測值 ,並根據過去的預測偏差信息，對其進行反饋校正，得到校正後的預測輸出 。
非線性模型預測控制基本原理
在非線性模型預測控制中，系統模型是非線性的，因此，相應的預測模型也是非線性的，設非線性系統的模型：
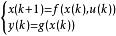非線性模型預測控制
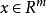非線性模型預測控制
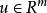非線性模型預測控制
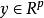非線性模型預測控制
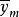非線性模型預測控制其中， ， ， 。根據這一模型，在 k 時刻只要知道對象的初始狀態x(k)及其未來的控制輸入 u(k),u(k+1),…，便可預測對象在未來各時刻的模型輸出 。
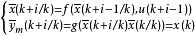非線性模型預測控制其中，i=1,2,...。
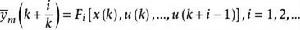非線性模型預測控制通過遞推，可以得到非線性系統的預測模型： 其中，是由 f(·)及 g(·)複合而成的非線性函式。
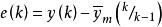非線性模型預測控制
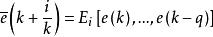非線性模型預測控制
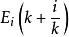非線性模型預測控制由於實際受控系統總包含某些不確定因素，利用上述模型預測，不能完全精確地描述對象的動態行為，因此可以在實測輸出的基礎上通過誤差預測和補償對預測模型進行反饋校正。記 k 時刻測得的實際輸出為 y(k)，則可由 構成預測誤差，並根據歷史的誤差信息 e(k),…,e(k-q)，通過誤差預測 校正基於模型的預測，並構成對輸出的閉環預測。其中， 為某一線性或非線性函式，其形式取決於所用的非因果預測方法，在 k 時刻，控制的目的是要求算出該時刻起的 M 個控制量 u(k), …u(k+M-1)(假設 u 在k+M-1 時刻後保持不變)，使輸出某一性能指標最優：
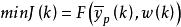非線性模型預測控制其中，
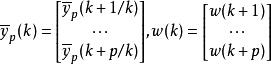非線性模型預測控制
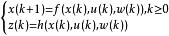非線性模型預測控制式中， w( k + i)為 k+i 時刻的期望輸出，M，P 的含義與線性預測控制相同。這樣，線上的滾動最佳化就是在閉環預測（下式）的約束下， 尋找控制作用使性能指標取極小的問題。如果可由此求出最優的u *( k ),...,u *( k + M− 1)，則在 k 時刻實施控制 u *( k )。到下一個採樣時刻，檢測系統的實際輸出進行誤差校正後，又重複進行最佳化，這就是非線性系統預測控制問題的一般描述。
常見的非線性預測控制方法
採用線性化方法
線性化方法是研究非線性系統的常規方法。將非線性系統局部線性化主要是為了沿用線性系統中已有的成果，計算簡單，實時性好。對於非線性較強的系統，用單個線性化模型很難反映系統在大範圍內的動、靜態特性，控制品質甚至穩定性都難以保證。因此實際處理時，有以下三種線性化方法。
（1）將非線性機理模型在每個採樣點附近線性化，然後對線性化的模型採用線性的預測控制算法，其特點是在每個採樣時刻都採用新的模型，能儘量減小線性化帶來的誤差。但是頻繁的線上更換模型會導致需要反覆計算相關矩陣參數，計算量加大，且不利於離線對控制器的參數進行最佳化設計。
（2）多模型方法。顧名思義，就是引入區間近似的思想，用多個線性化的模型來描述同一個非線性的對象。多模型方法的優點在於可以離線的計算大部分控制參數，難點則是如何確定模型切換的時機以及保證模型切換時的平穩性。
（3）反饋線性化（即就是 I/O 擴展線性化）的方法，即對非線性系統引入非線性反饋補償律，使非線性系統對虛擬控制輸入量實現線性化，便可以使用線性的 MPC方法。也有許多非線性系統不滿足反饋線性化的條件，使其套用受到限制。
利用各種特殊模型
常用的非線性模型包括 volterra 模型、Hammerstein 模型、Wiener 模型等。volterra模型為非線性對象的廣義脈衝回響模型，可以描述一類非線性對象的輸入輸出特性，實際套用中常採用正、負和雙階躍回響法建立系統的 volterra 模型。Hammerstein 模型和 Wiener 模型都是由一個非線性的靜態子系統和一個線性的動態子系統串聯而成，二者的區別是串聯的順序不同。
基於神經網路的預測控制
神經網路以其分散式存儲、並行處理、良好的魯棒性、自適應性、自學習性，在控制界具有廣闊的套用前景。由於神經網路能夠以良好的精度逼近非線性函式，且基於神經網路的建模方法具有普遍性，因此在非線性預測控制中受到重視，相關的研究成果也比較多。
關於採用神經網路的預測控制，存在的困難也比較多，主要是還不能有效地進行多步預測，而通常來說多步預測的控制效果要明顯優於單步預測。儘管將多個神經網路串聯可以得到多步的輸出預測，但這樣會增加控制器的複雜程度，直接影響控制量的求解。同時，如果需要線上進行模型辨識，那么線上的網路訓練需要較長的時間，控制的實時性變差。
非線性預測控制的難點
（1）非線性建模。建立一個用於非線性預測的高質量對象模型是提高預測控制性能的前提條件，由於控制器的設計是在模型先驗知識的基礎上進行，而控制器的性能也會受到建模誤差的影響。工業生產中對象的不確定性和大規模特性，使得非線性建模，特別是建立具有多步預測功能的模型，具有非常大的挑戰性和現實意義。
（2）滾動最佳化算法研究。線性的預測控制方法之所以能夠在工業上取得成功的套用，部分原因是這類問題的滾動最佳化都有有效的求解方法。非線性預測控制器每次採樣時刻都要求解一個非線性規劃，計算量大，而且缺乏有效的工具。研究一種適用性廣且效率高的最佳化算法，是一個具有挑戰性的課題。
（3）穩定性分析。在最佳化問題中加入穩定性約束（如終端約束或不等式約束、收縮約束），似乎從理論上解決了 MPC 的穩定性問題，但從工程套用意義上說，還沒有一種完全令人滿意的方法。首先，穩定性約束是人為附加的，可能會影響控制性能指標的實現；其次，穩定性約束將引起最佳化問題的可行性問題。
（4）過程套用。大多數非線性預測控制算法的套用還局限於各種仿真過程，現在迫切需要將理論研究成果推廣到實際過程套用中，能真正解決一些問題，並從中發現新問題，從而推動理論和實踐的前進。
