非線性模型的含義
 非線性模型
非線性模型如果解釋變數X的單位變動引起因變數的變化率(即斜率)是一個常數。則回歸模型是一種(解釋)變數線性模型。相反,如果斜率不能保持不變,則回歸模型就是一種(解釋)變數非線性模型。
非線性模型的一般形式是:
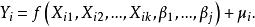 非線性模型
非線性模型 非線性模型
非線性模型 非線性模型
非線性模型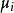 非線性模型
非線性模型 非線性模型
非線性模型式中,Y是被解釋變數;是 解釋變數;是 模型參數;為擾動項;是非線性函式。式中解釋變數的個數k與參數個數j不一定相等 。
變數非線性模型
 非線性模型
非線性模型Y與X之間不存線上性關係,但Y與參數之間存線上性關係。例如:
 非線性模型
非線性模型參數非線性模型
 非線性模型
非線性模型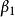 非線性模型
非線性模型Y與X之間存線上性關係,但是Y和參數之間不存線上性關係。例如,下面的模型是一個參數非線性模型,因為以平方的形式出現。
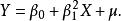 非線性模型
非線性模型對於非線性回歸分析,只有參數的線性回歸分析才是重要的,因為變數的非線性可通過適當的重新定義來解決 。
非線性模型的幾種情況
(1)Y與解釋變數不存線上。Y與未知參數也不存線上性關係,但可以通過適當的變換將其化為標準的線性叫歸模型。
例1柯布-道格拉斯生產函式。生產函式是指在一定時期內,在技術水平不變的情況下,生產中所使用的各種生產要素的數量與所能生產的最大產量之間的關係。也就是說,生產過程中總投入與總產出之間的一種函式關係。經濟學中,柯布-道格拉斯生產函式(C-D生產函式)是指產出表示為技術、資本和勞動投入量的函式。該生產函式由美國數學家柯布(C.W.Cobb)和經濟學家保羅·道格拉斯(Paul H.Douglas)共同創立而得名,是經濟學中普遍使用的生產函式。其形式為:
 非線性模型
非線性模型 非線性模型
非線性模型 非線性模型
非線性模型式中,Y表示產出;K和L分別表示資本投入和勞動力投入,A表示技術係數,和分別表示資本和勞動的產出彈性。
將C-D生產函式經對數變換。轉換為如下形式:
 非線性模型
非線性模型就可以利用線性模型中的OLS估計實現對生產函式中各係數的估計。
(2)Y與X不存線上性關係,Y與未知參數也不存線上性關係,而且也不能通過適當的變換將其化為標準的線性回歸模型。
在現實生活中,並非所有非線性函式形式都可以線性化,那些不能線性化的模型一般形式為:
 非線性模型
非線性模型 非線性模型
非線性模型比如,就是一個不能進行線性化處理的模型 。
其他解釋
非線性模型是反映自變數與依變數間非線性關係的數學表達式。設隨機變數為Y, 若可表示為:
 非線性模型
非線性模型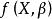 非線性模型
非線性模型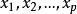 非線性模型
非線性模型 非線性模型
非線性模型 非線性模型
非線性模型 非線性模型
非線性模型此結構稱為 非線性模型, 其中為某種 非線性函式。Y為一隨機變數(依變數)的n次觀察值構成的n維向量。X為設計矩陣,由p個變數(自變數)的n次觀察值構成的n×p維向量,β為未知參數向量,e為隨機誤差向量,通常假設各觀測值是相互獨立且是同分布的,即。這裡,而也可以是未知的,這時它也是模型的未知參數, 稱為 誤差方差。
非線性模型的形式多種多樣, 依建立模型的方法不同可分為:① 推理模型。根據具體學科理論揭示的變數間相互關係用數學分析的方法建立模型, 如Logistic模型等,這類模型具有一定的生物學基礎,其參數具有確定的生物學意義。② 經驗模型。對某些變數無法推理方法得到或經推理得到但過於複雜的變數間關係,可利用適當的數學關係式直接擬合變數間關係,建立純經驗性模型,如奶牛泌乳曲線等,這類模型的參數多數沒有直接的生物學意義, 使模型的套用受到一定的限制。
依描述變數間關係的常用數學函式形式分為: 指數模型、 對數模型、 冪函式模型、 Logistic模型、 二次函式模型以及由此構成的 複合模型等。
處理非線性模型首先是建立或選擇適當的模型,然後是確定模型中所包含的參數, 其參數估計的基本原則仍是 最小二乘估計,方法通常有三種:① 變數變換法。通過某種數學轉換將非線性模型化為線性模型,即“曲線改直”或利用線性多項式逼近,該法簡單易行,具有一定的實用價值。② 非線性回歸法。根據最小二乘原則使誤差平方和最小,對非線性模型直接求解,常用的是Gauss-Newton法及在此基礎上改進的Marquardt法,可通過各種疊代法直接估計模型常數,這是目前處理非線性模型最為常用的方法。③ 直接最佳化法。直接利用非線性模型計算剩餘平方和並以其最小為最佳化目標函式尋求最優回歸係數, 常用的是單純形最佳化法。
在畜牧業中非線性模型常用於研究各種變數間的非線性回歸擬合、動物生長曲線、奶牛泌乳曲線及產蛋曲線等。隨著計算方法及手段的極大改進,非線性模型的套用得到迅速發展 。
幾種非線性模型的線性化
假定根據理論或經驗,已估計輸出變數與輸入變數之間的非線性表達式,但表達式的係數是未知的,要根據輸入輸出的n次觀測結果來確定係數的值。處理非線性回歸的基本方法是,通過變數變換,將非線性回歸化為線性回歸,然後用線性回歸方法處理。
指數函式模型
指數函式模型為:
 非線性模型
非線性模型對應的曲線為:
 圖1 指數函式曲線
圖1 指數函式曲線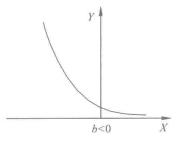 圖2 指數函式曲線
圖2 指數函式曲線 非線性模型
非線性模型 非線性模型
非線性模型令,則,得
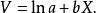 非線性模型
非線性模型 非線性模型
非線性模型 非線性模型
非線性模型令,則,得
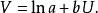 非線性模型
非線性模型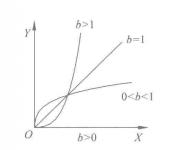 圖3 冪函式曲線
圖3 冪函式曲線 圖4 冪函式曲線
圖4 冪函式曲線對數函式模型
對數函式模型為:
 非線性模型
非線性模型對應的曲線如圖所示。
 圖5 對數函式曲線
圖5 對數函式曲線 圖6 對數函式曲線
圖6 對數函式曲線 非線性模型
非線性模型令,則
 非線性模型
非線性模型雙曲線函式模型
雙曲線函式模型為:
 非線性模型
非線性模型對應曲線如下。
 非線性模型 非線性模型 |  非線性模型 非線性模型 |
 非線性模型
非線性模型令,則
 非線性模型
非線性模型S型曲線函式模型
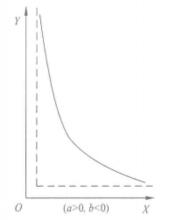
S型曲線函式模型為:
 非線性模型
非線性模型對應的曲線如下所示。
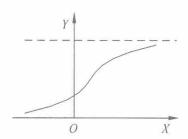 圖7 S型函式曲線
圖7 S型函式曲線 非線性模型
非線性模型令則
 非線性模型
非線性模型多項式模型
在只有一個自變數的情況下,多項式模型如下:
 非線性模型
非線性模型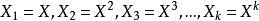 非線性模型
非線性模型令,則上述多項式可變換為多元線性模型:
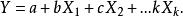 非線性模型
非線性模型
