背景
集合A中的一個等價關係～決定集合A的一個劃分，反之，給了集合A的一個劃分，便確定了集合A中的一個等價關係～。換言之，集合A的一個等價關係是A的任何劃分方式的基礎。
給了集合A的一個劃分後，便使每一元素a屬於A若且唯若屬於一個等價類[a]。也就是說，由等價關係給集合的分類是完備的。
事實上，對集合A的分類還有其他情形。
定義
定義 集合A的一個關係R叫做一個非自反關係，假如R滿足：
非自反關係(1)非自反性： a∈A=>aRa；
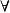非自反關係(2)對稱性： a，b∈A，aRb=>bRa；
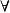非自反關係(3)傳遞性： a，b，c∈A，aRb，bRc=>aRc。
設R是A上的關係。若對所有a∈A，均有(a，a)∈ R，則稱R是A上的一個自反關係，也稱R是自反的或R具有自反性。如果R不是一個A上的自反關係，則我們稱R為A上的一個非自反關係，也稱R是非自反的。
相關定理
定理
集合A的一個不完全分類確定A的一個非自反關係R。反之亦然。
不完全分類
定義：設A為一個非空集合，如果A的一個子集族：{Al h∈N}滿足：
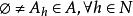非自反關係(1)
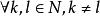非自反關係
非自反關係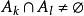(2)=>
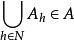非自反關係(3)
則稱集合集{Al h∈N}為A的一個不完全分類。
證明
設{Al h∈N}是A的某些非空子集的一個集合。定義關係R：aRb<=>存在惟一的h ∈N，使n ∈A。且b∈ A。
自反關係
在邏輯學和數學（離散數學）中，集合 X 上的二元關係 R 是自反的，若所有 a 屬於 X，a 關係到其自身。
表示
數學上表示為：對於任何a∈A，總有aRa，即任何 a∈A，使得（a,a）∈R，則稱集合A上的關係R是自反的。
例如："大於等於"是種自反關係，但"大於"不是自反關係。
舉例
自反關係舉例：
"等於"（等於）
"是……的子集"（集合的包含）
"小於等於"和"大於等於"（不等）
"除"（整除）
非對稱關係
.非對稱關係即反對稱的非自反關係。
滿足傳遞性的自反關係稱為預序關係。滿足反對稱性的預序關係稱為偏序關係。滿足對稱性的預序關係稱為等價關係。
X上的關係 R是非對稱的，若對所有的 a和 b屬於 X，若 a關係到 b，則 b不關係到 a。
數學上表示
任意 a,b 屬於 X，aRb -> 非（bRa）
定理
若一個關係是非自反的和傳遞的，那么它是非對稱的。
證明
設關係R滿足題目條件，所以<a,b>,<b,c>∈R那么<a,c>∈R。若他不是非對稱的，那么<a,b>,<b,a>∈R,由以上條件知，<a,a>∈R，所以與非自反矛盾，所以關係R是非對稱關係。
其他類似關係舉例
設關係為F(a,b)
自反性 = 對任意元素a證F(a,a)成立
反自反性 = 對任意元素a證F(a,a)不成立
對稱性 = 對任意兩個元素，若F(a,b)證F(b,a)成立
反對稱性 = 對任意兩個元素，若F(a,b)證F(b,a)必不成立
傳遞性 = 對任意三個元素，若F(a,b)且F(b,c)證F(a,c)成立
