基本概念
非慣性參照系就是能夠對同一個被觀測的單元施加作用力的觀測參照框架和附加非線性的座標系的統稱。非慣性參照系的種類無窮多。在經典機械力學中，任何一個使得“伽利略相對性原理”失效的參照系都是所謂的“非慣性參照系”。比如，一個加速轉動的參照系；一個加速振動的參照系；……；一個隨機任意加速運動的參照系等等。即任何一個使得牛頓第一定律和牛頓第二定律不再成立的參照系。在經典電動力學中，任何一個使得“愛因斯坦相對性原理”失效的參照系都是所謂的“非慣性參照系”。比如，任何一個使得洛侖茲電磁作用力定律F=qE+qu×B，或者麥克斯韋方程組不再成立的參照系。非慣性參照系與慣性力
經典力學對力定義相當簡單明了——力是物體對物體的作用，不錯，相當簡單明了！於是，人們認為只有具備兩個或兩個以上的物體才資格談力，凡是談到力則一定有施力物體，也有受力物體，這似乎與人們的生活實踐相一致。
可是，當人們坐在車上，並以車為參照系時，我們發現車上的物體居然可以無緣無故地加速運動起來，似乎有一個力作用在物體之上，這是一個什麼力呢？它具有什麼性質呢？施力物體是什麼？無論我們怎樣努力尋找，始終無法把這個力的施力物體找出來。為了弄清楚原因，我們下了車，在地面上以地面為參照系再來觀察一翻，這時，我們恍然大悟，原來當車一旦發生加速運動時，車上的物體就會在車相對於車廂加速運動起來，物體根本沒有發生運動而是保持靜止狀態，物體並沒有受到力的作用，當然我們找不到施力物體了。可見，在不同參照繫上觀察物體的運動，觀察的結果會截然不同！
於是，人們把參照系進行了分類，凡是牛頓第二定律能夠適用的參照系稱為慣性參照系，反之，牛頓第二定律不適用的參照系稱為非慣性參照系。牛頓第二定律所謂是否適用，我們考慮的因素實際上是力的產生條件，如果具備力的產生條件，則必然符合牛頓第二定律。通過總結，人們發現，凡是相對地面靜止或者做勻速直線運動的參照系都是慣性參照系，而相對於地面做變速運動的參照系是非慣性參照系；在眾多的慣性參照系中，相對地面靜止的慣性參照系具有特殊的優點，把它叫做絕對慣性參照系。
人們慣性參照系進行了諸多的討論同時，還對非慣性參照系進行了討論。一個物體在非慣性參照系中似乎在力作用下發生了加速運動，可是找不到其施力物體。為了迎合牛頓第二定律，人們假設了物體受到一個力的作用，這個力由物體的質量及其加速度的乘積決定，但是由於找不到施力物體，人們認為這不是一個真實存在的力，而是一個虛構的力，把這個力稱為“慣性力”。牛頓水桶實驗很明顯，
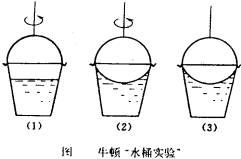牛頓水桶實驗“慣性力”大小取決於物體的加速度大小，而物體的加速度大小實際又取決於非慣性參照系相對於慣性參照系的加速度。那么，如何通過動力學實驗找到慣性系，從而確定任意一個對象的加速度呢？牛頓以“水桶實驗”來證實其可行性。當一個盛水的水桶帶著桶里的水轉起來的時候，水面會由平坦變成凹形，如果水桶停止轉動而水未停下，水面仍會呈凹形。如果建立一個與水相對靜止的轉動參照系，那么在這個參照系里水是靜止的，但這個參照系裡的實驗者卻會發現，似乎有一個向外的力維持著水面的形狀，不讓四周的水向中心回流，於是實驗者便可以下結論：我所在的系是個非慣性系，其中有慣性力維持著水面的凹形。推而廣之，只要在某個參照系裡，水靜止但水面不平坦，這就可作為非慣性系的判斷依據，這個非慣性系中存在著慣性力。牛頓認為，參照系中若發生這種情況，則說明它是一個相對於“絕對空間”有加速運動的參照系，並且通過動力學實驗可以測量出絕對的加速度。
然而這充其量只是一個判據，尚不足以說明慣性力究竟是從何而來的，曾經遭受過馬赫的強烈批判。後來的狹義相對論雖然否定了絕對空間，但也並沒有解決這個問題。另一方面，愛因斯坦嘗試將萬有引力納入狹義相對論框架時失敗了，他後來在馬赫原理的啟發下提出了等效原理和廣義相對性原理，取消了慣性系的優越地位，因此不再有必要區分慣性系與非慣性系，後來進一步建立了廣義相對論。
轉動的非慣性參照系與科里奧利慣性力
相對於慣性參照系做變速運動的參照系是非慣性參照系，在非慣性參照系中的物體會受到慣性力作用。轉動也是一種變速運動，而且是一種經常可見的變速運動，如果以一個相對於地面轉動的物體為參照系，那么物體在這個參照系中將受到兩種慣性力的作用——離心慣性力與科里奧利慣性力。而本文僅對科里奧利慣性力作相應的討論。
對於科里奧利力[1]，由於各方面的原因，筆者不能查閱與摘錄最原始的關於科里奧利力的論述文獻，在本文中謹摘錄了《力學基礎》（漆安慎、杜嬋英編寫，高等學校試用教材，高等教育出版社出版發行的1982年12月第1版）第125頁的論述：
如前所述，當質點靜止於勻速轉動的參照系中，在其中將觀察到質點受離心慣性力（也叫做慣性離心力，人民衛生出版社，胡新珉主編，醫學物理學第七版，P6）的作用。若質點相對於勻速轉動的參照系運動，則質點可能受到另一種慣性力，即科里奧利力。
參閱圖2.35，水平光滑可繞鉛直軸O轉動。設圓盤靜止，小球在合力為零的情況下，自盤上A尚半徑勻速運動運載B，無論從盤上盤下觀點，小球均有相同的運動狀態。假若圓盤現以恆定角速率轉動，而處於盤上A點的小球只具有與A點相同的線速度，則經過很短的時間，可近似認為小球相對於慣性系已從原來盤上A所在的點勻速運動至A所在的點C，如圖2.35(b)所示(注意有關圖上為明顯起見角度是誇大的).現在使圓盤轉動時小球同時參與上述由A至B和由A至C這兩種相對於慣性系的勻速直線運動,小球應到達圖2.35(c)中D點，與此同時，小球原來所在半徑已轉過一定角度，由AB轉至CD’，從圓盤上看，小球沒能保持在原來所在的半徑上而落後一定DD’。如果圓盤上有沿半徑方向內壁光滑的狹槽，情況就不同了。設在槽內且處於A點的小球相對於慣性系仍具有上述沿AB和AC的速度，但這時由於受到槽的約束，經過一很短時間，小球將到達D’點，從而補足自D至D’的位移，如圖2.36(a)所示，可見，在這一運動中，小球相對於慣性必然獲得某種與半徑垂直的附近加加速度，以補足位移DD’。
設小球沿半徑垂直方向作勻變速度運動，用表示附加加速度的大小，表示小球自A運動到D’的時間，則在時間內，圓盤的角位移為，又因考慮到小球沿槽作勻速運動，表示它相對於圓盤刻槽的速率，有故與上式對比得這一附加加速度是在慣性系中觀察到的，稱作科里奧利加速度，它產生於某相對相互作用力。質量為M的小球處於狹槽中，這個力只能是狹槽的邊緣所施的擠壓彈性力，此力應與狹槽垂直，且大小等於，如圖2.36(a)所示。
現從圓盤這一非慣性系觀察，小球僅沿槽作勻速度直線運動，按照牛頓第二定律，小球所受合力應為零。但小球已受到方才提到的力，故必存在一個慣性力與力平衡，則但方向與相反，非慣性參照系下的物理學屬性七定律及林氏三定律
筆者在諸多文章已經論述了物體在場環境中運動屬性，並且總結出物理學屬性七定律並在此基礎上又總結出林氏三定律；在自由粒子密度梯度場中，自由物體將做由密度梯度決定的屬性運動，屬性加速度與密度梯度成正比，其中等於在這種粒子中橫波的傳播速度的平方，是自由粒子的密度，是物體內部同種自由粒子的密度。這就是物理學屬性第零定律。
自由粒子在空間某一固定點的運動速度變化產生某點的速度變化率場，能夠自由粒子自由穿透的並且由這種粒子構成的自由物體在這種場中的運動加速度決定於物體所處位置的自由粒子的運動速度的變化，。這就是物理學屬性第一定律。
空間存在自由粒子的速度鏇度場，自由運動的物體將做由空間粒子速度鏇度與其物體的運動速度共同決定的屬性運動，屬性加速度分別與空間粒子速度鏇度和物體的速度成正比。這就是物理學屬性第二定律。
在自由的原子、分子溫度梯度場中，自由的物體將做由溫度梯度決定的屬性運動，屬性加速度與溫度梯度成正比。這就是物理學屬性第三定律。
在電性子密度梯度場中，自由電荷將做由密度梯度決定的屬性運動，屬性加速度與密度梯度成正比。對於電荷而言，這種場是一個庫侖電場或者是電壓分配電場，電場強度為。這就是物理學屬性第四定律。自由電荷在電性子空間中的加速勢決定於電荷所處位置的電性子速度的時間變化率。這是一個靜生林氏電場，場強為。這就是物理學屬性第五定律。
自由運動電荷的屬性加速勢將由電性子的速度鏇度與電荷的運動速度共同決定。這是一個動生林氏電場，場強為。這就是物理學屬性第六定律。
“力”是環境不平衡程度的反映，物體在不平衡的環境中必然地產生加速運動，“力”就等於物體質量與其屬性加速度的乘積，它是研究環境的不平衡程度與物體在相應環境中的屬性加速度的關係的中間物理量。筆者把這個定義稱為林海兵第零定律。
一切物體在平衡的環境中總是處於平衡狀態，直到環境由平衡向不平衡轉化迫使物體改變其原來的平衡狀態為止。這是林海兵第一定律。
一切物體在不平衡的環境中總是做加速運動，其加速度取決於各種環境不平衡的程度。這是林海兵第二定律。
在上述定律中，筆者用反抗速度矢量表示環境粒子的運動速度。
慣性力4科里奧利加速度的實質
人們都以為，科里奧利加速度是什麼非慣性力作用的結果，其實非也。這實際上是物質在中性子速度鏇度中的運動屬性而已，也就是物理學屬性第二定律所描述的情形。
其形成原因非常簡單——如果圓盤相對於地面在逆時針轉動時，那么，當以圓盤為參照系時，暗物質中性子則順時針以相同的角速度在鏇轉，在參照系空間內部形成了一定的速度鏇度，通過鏇度計算我們可以得到，是中性子在圓盤參照系中轉動的角速度矢量，根據物理學屬性第二定律可知，物體在這樣的參照系中的加速度為，即，是物體在圓盤參照系中的速度。這就是科里奧利加速度。
由此可知，在這樣的慣性系中，物體可能受到兩個環境屬性力——科里奧利力與離心力的作用。
廣義相對性原理
牛頓力學和狹義相對論中的相對性原理，其內容表述為“物理規律在一切慣性系裡具有相同的形式”，可以看出在牛頓力學和狹義相對論中，慣性系具有“優越性”，一個對象有沒有加速度依然是絕對的。而馬赫否認了絕對的加速度，認為加速度也是相對的，慣性力是相對於其他具體對象加速運動而產生的，而非相對於“絕對空間”。在馬赫原理和等效原理的基礎上，愛因斯坦提出了廣義相對性原理，巧妙地利用引力取消了慣性系的優越地位，認為“物理規律在一切參照系裡都具有相同的形式”，其數學方程在任意坐標系變換下形式都相同，這就是廣義協變性。這樣非慣性系與慣性系得以統一，大大增強了物理定律的普適性。
非慣性參照系附加引力場
考慮在高空向地球墜落的小物體，簡化為不考慮空氣和地球鏇轉的影響，那么分別選擇地球和小物體為參照系有：
以地球為參照系：由於地球近似為慣性系，所以小物體做自由落體運動，到達地面過程中動能不斷增加，其動能是由勢能轉換而來的，能量守恆成立。
以小物體為參照系：小物體是非慣性系，按照廣義相對論，其中有一個附加引力場，引力場指向上。地球在附加引力場作用下，沿著附加引力場方向加速運動，附加引力場對地球做功，地球的動能不斷增加，直至落到作為參照系的小物體上。作用於地球的附加引力場使地球動能增加，附加引力場的能量來自何方，用能量守恆怎樣解釋？
對於以垂直向上發射的火箭為參照系也有同樣的問題。
如果自由落體是一種特殊情況，沒有附加場。
那么，如果以水平加速的車作為參照系，就應該有附加場了。那么可以觀察到地球在向後加速運動，在這個參照系中，地球的動能增量是由什麼能源轉化而來的呢？
當然以地球為參照系的時候，車的動能增量是由發動機供給的。
