發展歷程
凸分析
研究凸集和凸函式的數學分支.其主要目的在於利用集合和函式的凸性來處理各種分析問題,特別是極值問題,包括有限維的數學規劃問題和無限維的變分學問題.其主要工具是凸集分離定理、次微分理論和對偶理論.
凸集的概念可以追溯到公元前3世紀的古希臘時代.當時,阿基米德(Archimedes)已定義凸弧為所有連結其上的點的弦都在同一邊的平面曲線.但是系統研究凸集理論是以19世紀末、20世紀初,德國數學家閔科夫斯基(Minkowski,H.)的工作為標誌的.閔科夫斯基對凸集的研究興趣起源於他對“數的幾何”問題(例如,一個平面集中至少有多少個坐標為整數的點)的研究.因此,他提出了用來刻畫一點到一個凸集距離——而現今稱為閔科夫斯基函式的概念,它尤其包括範數、半範數等凸函式作為特例.在他去世後的1911年發表的著作中,他對R中的閉凸集證明了凸集支撐定理.以後,卡拉西奧多里(Carathéodory,C.)等又進一步對凸集理論深入研究,尤其是在1911年提出R中的凸集可用n+1個點來表示的卡拉西奧多里定理.
凸函式概念的系統套用可從柯西(Cauchy,A.-L.)算起.現今,人們熟知的柯西不等式、幾何平均不大於算術平均等,都起源於柯西利用函式的凸性來證明不等式的研究.系統的凸性不等式研究是延森(Jensen,J.L.W.V.)的工作,他在1906年發表了這方面的專著.用作凸函式定義的不等式,通常稱為延森不等式.
對早期的凸性理論做出重要貢獻的還有黑利(Helly,E.).他在1917年證明而在1923年發表的黑利定理指出,如果R中的緊凸集族的任何n+1個集有非空交,那么整個族也有非空交.他甚至還在1921年,比哈恩(Hahn,H.)和巴拿赫(Banach,S.)更早地證明了哈恩-巴拿赫定理;這一涉及凸函式的線性泛函的延拓定理是與凸集支撐定理或凸集分離定理等價的.
20世紀50年代,既由於數學規劃、對策論、數理經濟學、最優控制等套用數學學科發展的需要,也由於泛函分析、變分學、位勢論等基礎數學學科發展的需要,凸性的研究變得越來越重要.1951年,芬切爾(Fenchel,W.)在美國普林斯頓大學印發了講義《凸錐、凸集和凸函式》,對凸集、凸錐和凸函式理論做了系統總結和發展.特別是把變分學中經典的勒讓德變換的概念推廣成為現今稱為勒讓德-芬切爾變換或共軛函式的概念,提出上圖、指示函式等運用方便的新概念.這些現今在凸分析中都成了基本概念.以後,克利(Klee,V.L.)又在一系列論文中對凸集理論做了深入的剖析.紹凱(Choquet,G.)則發展了1940年提出的克萊因-米爾曼定理(緊凸集是其端點集的閉凸包),而建立了現今的所謂緊凸集和凸錐的紹凱積分表示理論.1911年提出的布勞威爾不動點定理,也在這一時期被發展成為緊凸集中的連續映射的各種不動點定理.其中的代表是角谷靜夫1941年提出的緊凸集中的閉集值映射的不動點定理和樊(Ky Fan)從1952年起提出的一系列極小極大不等式.
凸分析真正被認為是相對獨立的數學分支,則是由於莫羅(Moreau,J.J.)和洛卡費勒(Rockafellar,R.T.)的工作.1967年莫羅的講義《凸泛函》和1969年洛卡費勒的專著《凸分析》被認為是凸分析的奠基著作.尤其是其中關於凸函式的次微分理論和對偶理論是使凸分析真正成為分析學科的一部分的標誌.莫羅的講義是在一般的局部凸拓撲線性空間的框架中敘述的,而洛卡費勒則更強調數學規劃理論中的套用,把凸分析局限在有限維空間中.以後又陸續出版了艾克蘭德(Ekeland,I.)和特曼(Teman,R.)的《凸分析和變分問題》(1974)等旨在針對變分學、最優控制等套用的巴拿赫空間上的凸分析著作.
20世紀70年代以後,凸分析又進一步發展為非凸分析、非光滑分析、集值分析等.許多凸分析的基本定理被推廣到非凸集和非凸函式情形.其中最引人注目的是洛卡費勒的學生克拉克(Clarke,F.H.)於1975年提出的關於局部李普希茨函式的廣義梯度理論.1994年起,國際上出版了第一本《凸分析雜誌》.按照該雜誌的發刊詞所說,廣義的凸分析理論,應包括凸分析的各種推廣,尤其是包括非光滑分析、集值分析等.
非凸分析(nonconvex analysis) 試圖把凸分析的基本理論和方法推廣到非凸集和非凸函式情形的數學分支.這個名稱現今已不常用,而代之為非光滑分析、集值分析等。
非光滑分析(nonsmooth analysis) 凸分析的發展.凸分析的次微分理論使得人們能夠對非光滑凸函式推廣微分法來處理極值問題.非光滑分析就致力於更一般的廣義微分法,來處理非光滑函式的極值問題.這方面現今最成功的是克拉克(Clarke,F.H.)對局部李普希茨函式提出的廣義梯度理論.他在1983年出版的《最最佳化和非光滑分析》一書已成為這方面的經典著作。
集值分析(set-valued analysis) 以集值映射為研究對象的數學分析.點對應集合的集值映射是很早就出現的數學概念.但長期來雖有少量研究,卻常被人認為不很重要.20世紀50年代以後,由於數理經濟學、數學規劃理論等的發展,使集值映射概念在其中起本質作用.例如,需求映射、供給映射等作為價格的函式都不是單值的;數學規劃問題解的穩定性問題,也涉及解集合(一般的數學規劃問題的解沒有惟一性)作為參數的集值映射的連續性.凸分析中出現的導數概念的推廣——次微分映射也不是單值映射,而是集值映射.這樣,就逐漸形成集值分析這個新的分支.1990年,奧邦(Aubin,J.P.)和弗朗科斯卡(Frankowska,H.)出版了《集值分析》一書,初步總結了集值分析的已有成果.1994年,國際上出版了《集值分析雜誌》。
概念體系
對於每一種微分和梯度概念,從它的泛函分析和非光滑幾何學角度進行歸納與總結,以便建立它們之間的內在聯繫和數學本質。如表所示,表中的各個概念形成了非光滑分析的體系 。
非光滑分析的概念體系
| 凸切錐 | Clarke相依錐 | 相依錐 |
| 方嚮導數 | Clarke 廣義方嚮導數 | 相依上導數 |
| 次微分的對偶定義 | Clarke廣義梯度 | 相依次微分(或稱相依廣義梯度) |
| 次微分的線性近似定義 | (粘性)下導數 |
基本概念
非光滑分析的基本概念
次微分、Clarke廣義梯度、下導數Dˆf(X)和相依上導數D↑f(x;v)分別是凸分析理論、非光滑分析理論、粘性解理論和生存理論中處理非可微函式的重要概念,它們的定義如下 :
(1)次微分af(X):
假定f(X)為凸函式,則函式在x點的次微分af(X)定義為:
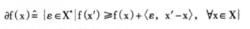 非光滑分析
非光滑分析(2)Clarke廣義梯度afc(x):
假定f(x)在x點是Lipsehitz連續的,則函式在x點的Clarke廣義梯度afc(X)定義為:
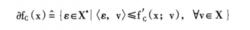 非光滑分析
非光滑分析其中f'c(x;v)為Clarke廣義方嚮導數:
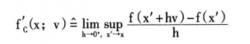 非光滑分析
非光滑分析(3)上導數D﹢f(x)和下導數Dˉf(x):
假定f(x)在X點上可微或下可微,則函式在x點的上導數D+f(x)和下導數Dˉf(x)的定義為:
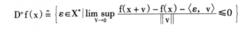 非光滑分析
非光滑分析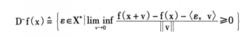 非光滑分析
非光滑分析(4)相依上導數D↑f(x;v)和相依下導數D↓f(x;v)
假定f(x)在x點是相依上可導的,則函式在x點的相依上導數D↑f(x;v)和相依下導數D↓f(x;v)分別定義為:
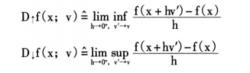 非光滑分析
非光滑分析上述微分和梯度的定義方式各不相同,有用線性近似效果定義的,有用對偶集定義的,還有用極限方式定義的。不同的定義方式代表了不同理論背景(泛函分析、凸分析和集值分析等),雖然它們的描述方式差別很大,但它們之間是有內在聯繫的(Clarke,1983;Aubin,1990;王春峰,1994;Frankowska,1989,1993)。
在凸分析中,對於凸函式,設方嚮導數
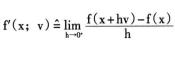 非光滑分析
非光滑分析則次微分有如下性質:
(1)v→f’(x;v)是正齊次,次可加凸函式。
(2)式:
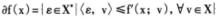 非光滑分析
非光滑分析表明方嚮導數是次微分的支撐函式。
(3)af(·)是非空凸緊集。
由上可知,正齊次、次可加的方嚮導數v→f’(x;v)控制著一個線性泛函集——次梯度集(這正是著名的Hahn—Banach定理的結論)。非光滑分析正是利用此特性來定義多種廣義梯度的。對於一般非光滑函式,方嚮導數v→f’(x;v)不是凸的,這時應首先凸化方嚮導數,得到一個正齊次、次可加的凸函式——廣義方嚮導數,然後定義出其對偶集——廣義梯度。Clarke廣義方嚮導數和Clarke廣義梯度就是用這種方式定義的。相依上導數也可以用這種方式定義相依次微分的概念。
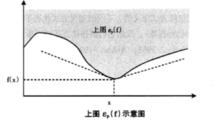
上述的方嚮導數都具有一定的幾何意義,一般都是用函式上圖和切錐描述的。上圖的作用是將函式概念轉換成集合概念。在一定條件下,方嚮導數的上圖是函式上圖的切錐,這種幾何解釋不僅使各種方嚮導數和廣義梯度的含義更加直觀,還可以重新定義廣義梯度概念。事實上,生存理論中的相依上導數就是用這種方式得到的。相依錐是切錐概念的推廣,K集合在x點的相依錐Tk(x)可用集合上極限定義為:
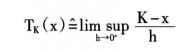 非光滑分析
非光滑分析如圖所示,它是集合K在x點的一種“內方向”集合。相依上導數的幾何解釋就是:相依上導數的上圖是函式上圖的相依錐。
 非光滑分析
非光滑分析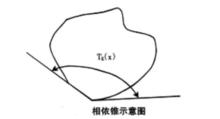 非光滑分析
非光滑分析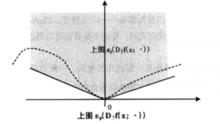 非光滑分析
非光滑分析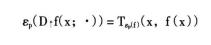 非光滑分析
非光滑分析非光滑分析的基本概念間有如下關係:
(1)不可微函式的各種廣義導函式都是正齊次泛函,它們的上圖是各類幾何錐體。當導函式為正齊次、次可加泛函(又稱次線性泛函)時,這些錐是凸錐,在集值分析中有很好的性質。同時根據Hahn—Banach定理,x上的次線性泛函控制著X上的線性泛函(ε,v)≤f’(x;v),即次微分。由此定義的對偶集都是閉凸集,便於利用成熟的凸分析最佳化技術。
(2)當函式f(x)是F可微函式時,所有上述廣義方嚮導數都等於(f’(x),v),其中f’(x)是x點的Frenchet導數,上圖的各種切錐都擴展成f’(x)在x點的切平面、切空間,所有的各種廣義導數次微分都變成單點梯度集且等於Frenchet導數f'(x)。
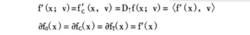 非光滑分析
非光滑分析(3)當函式f(X)是凸函式時,所有上述廣義方嚮導數都等於X點的方嚮導
數,各種切錐都成為凸分析中的閉凸切錐,所有的廣義導數次微分梯度都等於凸
分析中的次微分。
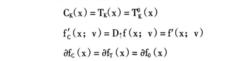 非光滑分析
非光滑分析(4)當函式f(X)是上柔滑函式時,相依錐與Clarke相依錐、相依上導數與
Clarke廣義方嚮導數、相依次微分與Clarke廣義梯度的關係如下(Aubin,1990) :
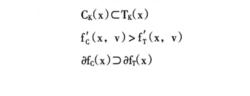 非光滑分析
非光滑分析
