基本介紹
旨在理論上對電力系統進行整體上的建模和分析，建立對電力系統的理論認識。
chapter1:現代電力系統的基本特性
1.1 發展歷史
第一個完整電力系統的締造者——托馬斯*愛迪生
第一台商用的HVDC輸電於1954年在瑞典堅持
1.2 電力系統的結構
1.輸電系統 2.次輸電系統 3.配電系統
1.3 電力系統控制
需要滿足的要求：1.適應符合有功與無功功率的需求
2.成本最低
3.供電質量（包括電壓、頻率、可靠性）
chapter2：電力系統穩定問題導論
2.1電力系統穩定定義：即電力系統的一種特性，即它能夠運行於正常運行條件下的平衡狀態，在遭受干擾後仍能夠恢復到可以運行的平衡狀態。
2.1.1 轉子角穩定
問題的基本因素：同步電機的功率輸出隨其轉子隨其轉子搖擺變化的關係。
穩定性現象
即將系統受到干擾時，描述系統的物理量是一個隨時間變化收斂的函式：
即∑（t→∞）F(t)=const
定理公式
一.磁路定理
二.電磁感應定律
線圈中通過的磁鏈發生變化時，線圈兩端會產生感應電壓，兩種的關係可用下公式表達：
E=-dψ/dt
該公式反映了以下信息：
1.E與ψ的數量關係。
2.E與ψ方向的確定。
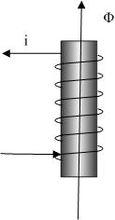電力系統學習由上圖可以得出等效電路圖：
電力系統學習三.磁鏈&電流的關係
當磁鏈的正方向與電流的正方向相同時（即符合右手螺旋定則），兩者的關係可以下公式表示：
ψ=Li
當磁鏈的正方向與電流的正方向相反時（與右手螺旋定則相反），則在公式前要加一負號：
ψ=-Li
所以，ψ與i之間的這種關係也可以表示成一種路的形式，當通過線圈的磁鏈由不同部分組成時，而這些磁鏈都是由不同的磁勢產生時，可用公式表示這種關係（ψ_ij表示F_j在第N_i個線圈產生的磁鏈）
所以有：ψ_ij=N_i φ_j
所以所有通過第N_i個線圈的磁鏈可以表示為：
ψ_i=∑（j=0-N）L_ij×I_j
所以，當電路中存在磁路時，可將其表示成磁鏈與電流的關係，然後再由電磁感應定律轉換成電壓和電流間的關係。
四.討論線圈磁電關係及列寫方程的步驟：
1.以每個線圈為基本的研究對象，分析通過該線圈的磁通。
2.列寫磁鏈關於電流的關係式
3.標麼化、折算，並畫等效磁路圖。
4.列寫磁路方程，電路方程，畫等效電路圖。
對於某個線圈，假設第i個線圈，通過該線圈的磁通包括兩部分
1.自身電流產生的磁通（包括主磁通與漏磁通）
2.其它線圈通過第i個線圈磁通的總和。
下面以雙繞組變壓器為例推到其磁電方程
a.原邊線圈1
其包括主磁通 φ_m與漏磁通φ_σ1
其中φ_m=φ_m1+φ_m2
又φ_m1=N_1*i_1*P_m，φ_m2=N_1*i_2*P_m，φ_σ1=N_1*i_1*P_σ1
ψ_1=N_1^2*P_σ1*i_1+N_1^2*P_m*i_1+N_1*N_2*i_2*P_m
=N_1^2*i_1*(P_σ1+P_m)+N_1*N_2*i_2*P_m
同理：
ψ_2=N_2^2*i_2*(P_σ2+P_m)+N_1*N_2*i_1*P_m
令 L_11=N_1^2(P_σ1+P_m) L_12=L_21=N_1*N_2*P_m L_22=N_2^2*(P_σ2+P_m)
可得磁鏈-電流方程式：
ψ_1=L_11*i_1+L_12*i_2
ψ_2=L_21*i_1+L_22*i_2
也可得到電壓方程：
u_1=-pψ_1+i_1*r_1
u_2=-pψ_2+i_2*r_2
通過分析磁鏈電流方程：
ψ_1=N_1^2*P_σ1*i_1+N_1^2*P_m*i_1+N_1*N_2*i_2*P_m
=N_1^2*P_σ1*i_1+N_1^2*P_m*i_1+N1_2*P_m*(N_2*i_2/N_1)
設i_2'=N_2*i_2/N_1
ψ_1=N_1^2*P_σ1*i_1+N_1^2*P_m*i_1+N_1^2*P_m*i_2'
=(L_σ1+L_m1)i_1+L_m1*i_2'
=L_σ1*i_1+L_m1*(i_1+i_2)
可把該種關係表示成等效圖：
（圖）
同理：
ψ_2=N_2^2*i_2*(P_σ2+P_m)+N_1*N_2*i_1*P_m
=N_2^2*(N_2*i_2/N_1)*N_1/N_2+N_1*i_1*Pm
由於ψ與電勢存在著線性關係所以，也應該對其進行等效
k*ψ_2=N_1^2*P_σ2*i_2'+N_1^2*P_m*i_2'+N_1^2*P_m*i_1
ψ_2' = L_σ2'*i_2'+L_m1*i_2'+L_m1*i_1
= L_σ2'*i_2+L_m1*(i_1+i_2')
所以，雙繞組的磁鏈電流關係可以等效為：
圖？？
磁鏈電流的關係，對其取導，可得到:
u_1 =L_σ1*di_1/dt+L_m1*(di_1/dt+di_2/dt)
u_2'= L_σ2''*di_2'/dt+L_m1*(di_1/dt+di_2'/dt)
在加上銅耗（r1,r2）及鐵耗（r_m）：
u_1=r1*i_1+r_m*(i_1+i_2')+ L_σ1*di_1/dt+L_m1*(di_1/dt+di_2/dt)
u_2'=r2*i_2'+r_m*(i_1+i_2')+L_σ2''*di_2'/dt+L_m1*(di_1/dt+di_2'/dt)
因此，可的到雙繞組的等效電路圖：
（圖）
現在討論同步發電機的電磁關係：
同步發電機的定子磁勢和轉子磁勢是同步旋轉的，在一般情況下，定子磁勢與轉子磁勢是成一定夾角的，所以可以
把定子磁勢分解成兩個互相垂直的磁勢——一個與轉子磁勢方向一致，另一個與轉子磁勢相垂直
分析步驟
電力系統的分析步驟：
1.建立電力系統各模組模型。
2.在模型的基礎上分析系統的性能。
證明方法
在此處添加文本內容
相關人物
編輯者：羅夢澤
在此處添加文本內容
相關理論
高等數學、工程數學
【2】 電力系統穩定與控制
【3】 電機學
【4】 自動控制原理
【5】 複變函數與積分變換 在此處添加文本內容
