簡介
隨著計算機技術的高速發展和工業自動化等領域的實際需要，控制算法的實現經常需要採用數字計算機，但當採用數字計算機實現滑模變結構控制算法時，由於採樣過程的限制，理想的滑動模態是不存在的，狀態運動軌跡只能以抖振形式在切換面的某一鄰域內運動並漸近趨向原點或原點的一個鄰域。
所以，對於離散時間系統，滑模變結構控制不能產生理想的滑動模態控制，只能產生準滑動模態控制。在離散時間情況下，滑動模態的性質、存在及到達條件都己改變。
對離散時間系統建立變結構控制，其基本原理和連續系統完全一樣，也分為兩個基本內容：
(1) 選擇切換函式 s ( x )= Cx，使得其上的滑動模態全局漸進穩定；
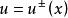離散滑模變結構控制(2) 求變結構控制 ，使得所有運動均於有限時間內到達切換面s ( x ) = 0。
描述
將連續時間系統狀態方程離散化，可得離散時間系統的狀態空間方程：
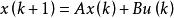離散滑模變結構控制
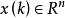離散滑模變結構控制
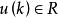離散滑模變結構控制
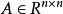離散滑模變結構控制
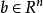離散滑模變結構控制其中， 為系統的狀態， 為控制輸入， ， ，假設(A，b)完全可控。
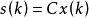離散滑模變結構控制
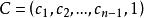離散滑模變結構控制選擇切換函式： ，其中，
連續時間系統的滑模變結構控制中討論三個基本問題：滑動模態的存在性、可達性及穩定性。這也是離散時間系統滑模變結構控制的基本問題，但離散時間系統自身的固有特點使得其與連續時間系統有所不同。
到達條件
選定了切換函式後，接下來需要確定到達條件，以保證任意初始狀態出發的運動於有限時間到達切換面。通常在連續情形下，到達條件主要分為兩類：不等式型和等式型。離散情形下的到達條件，大多是對連續情形的推廣，曾經提出過以下形式的到達條件。
不等式型
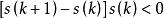離散滑模變結構控制
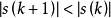離散滑模變結構控制
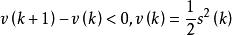離散滑模變結構控制離散時間指數趨近律
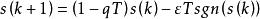離散滑模變結構控制離散時間指數趨近律：
離散滑模變結構控制其中， ，q>0，qT<1。
離散時間指數趨近律作為滑模變結構控制的到達條件與一般不等式型到達條件的區別在於：考慮到了採樣周期的影響。離散時間指數趨近律具有一下優點：
（1）滿足滑模變結構控制到達條件的六個要求；
離散滑模變結構控制（2）保證系統在趨近模態階段具有良好的品質，並且趨近律中的參數 與q可以調節；
（3）切換帶的大小可以計算；
（4）使求解滑模變結構控制問題變的異常簡單；
（6）等式型的到達條件給出等式型的變結構控制，設計起來非常簡單。
準滑動模態
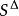離散滑模變結構控制
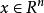離散滑模變結構控制
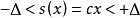離散滑模變結構控制定義一個包圍切換面的切換帶：={|}。
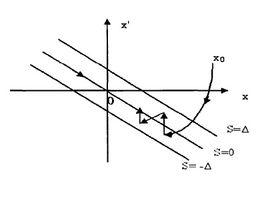
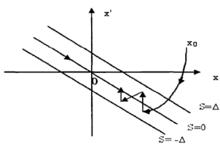圖1 準滑動模態圖
離散滑模變結構控制從任意初始狀態出發的離散時間系統的運動，或者在有限步內到達切換面s，然後在切換面上運動，這種情況稱之為理想的準滑動模態；或者在切換帶內運動，系統狀態步步穿越切換面，這種情況稱之為非理想的準滑動模態。系統發生在切換帶內的上述兩種準滑動模態，稱之為離散時間系統滑模變結構控制的準滑動模態。2稱為切換帶的寬度，如圖1所示。
在離散時間系統滑模變結構控制中，從任意狀態出發的運動可分為以下三個階段：
(1) 趨近模態：從初始狀態趨向切換帶階段。
(2) 準滑動模態：分為兩種情況，或者為理想的，或者為非理想的準滑動模態。
(3) 平穩狀態：或為原點x=0，屬於理想準滑動模態；或為圍繞原點的抖振，屬於非理想狀態。
在離散時間系統滑模變結構控制中，從任意狀態出發的運動應滿足如下特性：
(1) 運動從任意初始狀態出發後，一定要單調地向切換面趨近，並在有限時間內到達切換面或穿越切換面。
(2) 運動一旦穿越切換面，它的每一個後續步驟均從另一面穿越切換面，並一直進行下去。
(3) 運動穿越切換面開始後，每一步的長度是遞減的，運動軌跡限定於一特定帶內。
離散滑模變結構控制的不變性
滑模變結構控制的最突出特點是可以實現滑動模態與參數攝動和系統的干擾完全無關，即是滑動模態的不敏感性，正是這種不敏感性使滑模變結構控制受到廣泛的重視。但對於一般線性系統來說，這種不敏感性的成立是有條件的，那就是必須滿足匹配條件。
離散時間系統滑模變結構控制由於受採樣周期的影響，所以其滑動模態相對於連續時間系統的滑動模態來說，情況是相當複雜的。在此給出三點結論。
對於如下形式的離散時間不確定性系統：
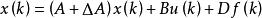離散滑模變結構控制
離散滑模變結構控制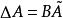
離散滑模變結構控制
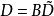離散滑模變結構控制其中，為參數攝動，f(k)為外界干擾，一般來說都不可測的。假設系統滿足參數攝動及外界干擾的匹配條件：，，那么以下結論成立：
(1) 當不確定項和外界干擾滿足匹配條件時，理想準滑動模態對參數攝動和外界干擾是無關的。
(2) 在非理想準滑動模態下，無論參數攝動和外界干擾是否滿足匹配條件都不具有這種不敏感，因為在此滑動模態下，趨近過程和準滑動模態均與參數攝動和外界干擾有關。
(3) 可以證明理想準滑動模態對參數攝動和外界干擾具有不敏感性，這隻要求參數攝動及外界干擾有界，且其界不大的情況下。
