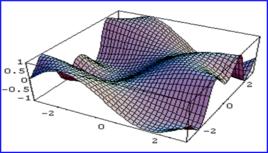
概念
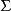 雙側曲面
雙側曲面 雙側曲面
雙側曲面 雙側曲面
雙側曲面 雙側曲面
雙側曲面 雙側曲面
雙側曲面在光滑曲面 上任取一點 ,過點 的法線有兩個方向,如果選定法線的某個方向為指定的方向,當點在曲面上連續移動時,法線也連續變動、當動點從 出發沿著曲面上任意一條不越過曲面邊界的封閉曲線又回到原位置 時,法線的指向保持不變,稱這種曲面為雙側曲面。
基本原理
性質
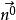 雙側曲面
雙側曲面 雙側曲面
雙側曲面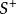 雙側曲面
雙側曲面 雙側曲面
雙側曲面(1)由於第二類曲面積分是在雙側曲面指定的一側進行的,如果考慮不同的側面,此時 的方向相反,因而面積的投影相差一負號,若記曲面 的某一側為 ,相反一側為 ,則
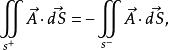 雙側曲面
雙側曲面因此,當改變曲面的側,積分改變符號,這與第一類曲面積分是一個顯著差別。
對於曲面的側,若曲面非封閉,可分為上側與下側,前側與後側,左側與右側;若曲面封閉,則可分為外側與內側。
 雙側曲面
雙側曲面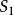 雙側曲面
雙側曲面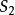 雙側曲面
雙側曲面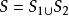 雙側曲面
雙側曲面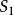 雙側曲面
雙側曲面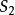 雙側曲面
雙側曲面(2)若曲面 分為兩塊曲面 與 ,即 , 與 沒有公共內點,但不改變曲面的側,則
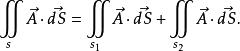 雙側曲面
雙側曲面計算法
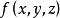 雙側曲面
雙側曲面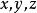 雙側曲面
雙側曲面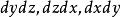 雙側曲面
雙側曲面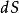 雙側曲面
雙側曲面第二類曲面積分可化為二重積分來計算,但須注意到被積函式中的變數應滿足曲面方程,是面積元素分別在各坐標面上的投影,計算公式為
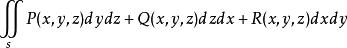 雙側曲面
雙側曲面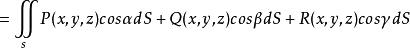 雙側曲面
雙側曲面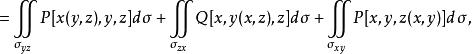 雙側曲面
雙側曲面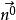 雙側曲面
雙側曲面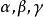 雙側曲面
雙側曲面 雙側曲面
雙側曲面 雙側曲面
雙側曲面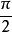 雙側曲面
雙側曲面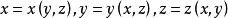 雙側曲面
雙側曲面 雙側曲面
雙側曲面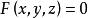 雙側曲面
雙側曲面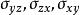 雙側曲面
雙側曲面其中,當法線矢量的方向角為銳角時,相應積分號下取“”號;為銳角時取“”號,特別,若為時,則相應積分值為零。而是曲面的方程的三種表示,它們分別在上都是單值連續函式。