集函式

集函式是測度論中定義的概念，是以集類為定義域的函式。關於集函式，也可引入單調性、收斂性等概念。

簡介

集函式是測度論中定義的概念，是以集類為定義域的函式。

設是Ω上的一個集類，K是實數域或複數域，稱映射μ:→K為定義在上的集函式。重要的（數值）集函式有測度、集上的積分等。若實值集函式的值可允許取+∞或-∞，則稱此集函式為擴充實值集函式。

性質

關於集函式，也可引入單調性、收斂性等概念。

例如，設μ是定義在集類上的實值集函式，如果對任意A,B∈，A⊂B，均有μ(A)≤μ(B)，則說μ在上是單調增加的。

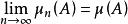集函式

設{μ}是集類上的集函式列，若對於每個A∈，數列{μ(A)}收斂，則說{μ}在上收斂。若對於每個A∈，有，則稱{μ}在上一致收斂於μ。

向量值集函式

當K是向量空間或運算元集時，分別稱映射μ:→K為上的向量值集函式或運算元集函式。

常見的這種集函式有向量值測度、譜測度和譜積分等。