定義
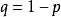 隨機遊動
隨機遊動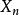 隨機遊動
隨機遊動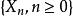 隨機遊動
隨機遊動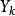 隨機遊動
隨機遊動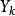 隨機遊動
隨機遊動隨機遊動亦稱隨機徘徊。一種最基本的整值隨機過程。假定一質點在數軸的整點上做如下運動:每次質點以機率 p 向右 1 單位;以機率向左 1 單位,且各次運動相互獨立。以表示時刻 n 質點的位置,則過程稱為隨機遊動,由假設表示質點的第 k 次位移,由假設 {} 獨立分布:
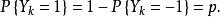 隨機遊動
隨機遊動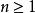 隨機遊動
隨機遊動而對,有
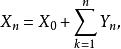 隨機遊動
隨機遊動於是它是平穩獨立增量過程,從而是離散時間時齊馬爾可夫鏈,其一步轉移機率為
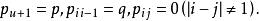 隨機遊動
隨機遊動若質點可以在整個數軸的整數點上遊動,則稱這種隨機遊動為無限制隨機遊動。若在某點D設有一個吸收壁,質點到達這點即被吸收而不再遊動,因而整個遊動也就結束了,這種隨機遊動稱為在D點有吸收壁的隨機遊動,若P=Q=1/2,隨機遊動稱為對稱的。
隨機環境中的隨機遊動
[random walk in random environments]
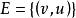 隨機遊動
隨機遊動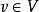 隨機遊動
隨機遊動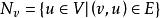 隨機遊動
隨機遊動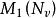 隨機遊動
隨機遊動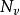 隨機遊動
隨機遊動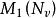 隨機遊動
隨機遊動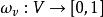 隨機遊動
隨機遊動設(V,E)是無窮的有向圖,具有可數的頂點集 V 和邊集。對任意,定義它的鄰域(neighborhood),表示支撐為的 V 上的機率測度全體。中的元素稱為在 v 點的轉移律(transition law),是定義在 V 上的可測函式滿足如下條件:
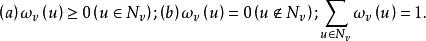 隨機遊動
隨機遊動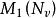 隨機遊動
隨機遊動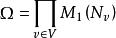 隨機遊動
隨機遊動在上賦予機率測度的弱拓撲使其為波蘭空間(Polish space),進而誘導出上的波蘭結構,以F 表示Ω上的博雷爾σ代數。給定(Ω,F)上的一個機率測度P ,一個隨機環境(random environment)就是取值在Ω中的一個隨機變數ω,其分布為 P。
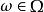 隨機遊動
隨機遊動對任意,定義隨機環境ω中對隨機遊動(random walk in random environment ω)為取值在 V 中的時齊馬爾可夫鏈,其轉移機率為
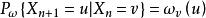 隨機遊動
隨機遊動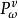 隨機遊動
隨機遊動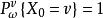 隨機遊動
隨機遊動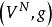 隨機遊動
隨機遊動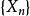 隨機遊動
隨機遊動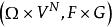 隨機遊動
隨機遊動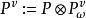 隨機遊動
隨機遊動以表示滿足初始條件在上誘導的機率,稱為隨機遊動的淬火機率(quenched law)。在上定義為
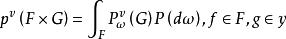 隨機遊動
隨機遊動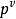 隨機遊動
隨機遊動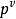 隨機遊動
隨機遊動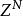 隨機遊動
隨機遊動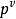 隨機遊動
隨機遊動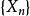 隨機遊動
隨機遊動在不引起混淆的情況下,也以記在上的邊際分布,稱為隨機遊動的退火機率(annealed law)。

