術語介紹
通常,我們可假設隨機漫步以馬爾可夫鏈或馬爾可夫過程形式出現,但比較複雜的隨機漫步則不一定以這種形式出現。在某些條件限制下,會出現一些比較特殊的形式。如醉漢走路(Drunkard's walk)或萊維飛行(Levy flight);在平面和空間內多維的無規活動;有些則可成群,有些還和時間參數有關,隨機時間發生等。氣體或液體中分子活動的軌跡;金融價格漲落,賭場中的錢財狀態等都可作為隨機漫步的模型。
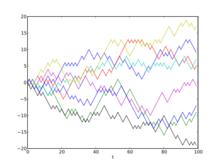 圖1.一維的隨機遊走。縱軸表示當前的位置,橫軸表示時間步數。
圖1.一維的隨機遊走。縱軸表示當前的位置,橫軸表示時間步數。隨機漫步和擴散模型有關,是馬爾可夫過程討論的基本過程。目前已在許多領域套用:生態學、經濟學、心理學、計算科學、物理學、化學和生物學等。它們用來說明這些領域內觀察到的行為和過程,因而是記錄隨機活動的基本模型。
隨機遊走
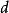 隨機漫步
隨機漫步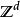 隨機漫步
隨機漫步流行的隨機漫步模型是在規則格上隨機漫步的模型,其中每個步驟根據機率分布跳轉到另一個站點。在簡單的隨機漫步中,位置只能跳到格子的相鄰位置,形成一個格子路徑。在局部有限格上的簡單對稱隨機漫步中,跳轉到其鄰居中的每一個的機率是相同的。研究最好的例子是在 維整數格線(有時稱為超立方體格線)上隨機遊走, 。
如果狀態空間限於有限維度,隨機遊走模型被稱為簡單有界對稱隨機漫步,並且轉移機率取決於狀態的位置,因為在邊緣和角落狀態下運動是有限的。
一維隨機遊走
隨機遊走的一個基本例子是整數線上的隨機遊走,從0開始,每一步以相同的機率移動+1或-1。
這一步可以說明如下。數字線上的標記被置於零,並且公平的硬幣被翻轉。如果它落在頭上,則標記向右移動一個單位。如果它落在尾巴上,標記會向左移動一個單位。五次翻轉後,標記現在可以在1,-1,3,-3,5或-5上。有五個翻轉,三個頭和兩個尾巴,以任何順序,將登入1.有1種方式(翻轉三個頭和兩個尾巴),10個著陸方式-1(通過翻轉三個尾巴和兩個頭),3個著陸方式(通過翻轉四個頭部和一個尾部),5個著陸方式-3(通過翻轉四個尾部和一個頭部),一個著陸方式5(通過翻轉五個頭部)和-5的一種登入方式(通過翻轉五個尾巴)。
 圖2.所有可能的隨機遊走結果5次公平硬幣翻轉後
圖2.所有可能的隨機遊走結果5次公平硬幣翻轉後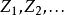 隨機漫步
隨機漫步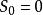 隨機漫步
隨機漫步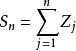 隨機漫步
隨機漫步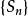 隨機漫步
隨機漫步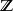 隨機漫步
隨機漫步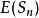 隨機漫步
隨機漫步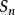 隨機漫步
隨機漫步為了正式定義這個散步,需要獨立的隨機變數 ,其中每個變數是1或-1,對於任一值和50%的機率 和 。該系列 被稱為簡單的隨機遊走 。如果步行的每個部分的長度都是1,則該序列(-1s和1s的序列的總和)給出步行的距離。該預期 的 是零。也就是說,隨著翻轉次數的增加,所有硬幣翻轉的平均值接近零。這遵循期望的有限可加性性質:
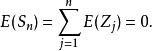 隨機漫步
隨機漫步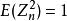 隨機漫步
隨機漫步一個類似的計算,使用隨機變數的獨立性和事實 表明:
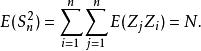 隨機漫步
隨機漫步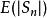 隨機漫步
隨機漫步 隨機漫步
隨機漫步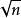 隨機漫步
隨機漫步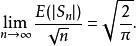 隨機漫步
隨機漫步 隨機漫步
隨機漫步這暗示了 中,預計後平移距離步驟,應該是順序的 。實際上,這個結果表明擴散對於混合是無效的,因為平方根的表現方式很大。
馬爾可夫鏈
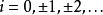 隨機漫步
隨機漫步 隨機漫步
隨機漫步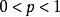 隨機漫步
隨機漫步 隨機漫步
隨機漫步 隨機漫步
隨機漫步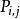 隨機漫步
隨機漫步一維 隨機漫步也可以看作一個馬爾可夫鏈,其狀態空間由整數給出。對於一些數滿足,轉移機率(從狀態 移動到狀態 的機率)由下式給出:
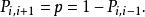 隨機漫步
隨機漫步假說
隨機遊走假說(Random walk hypothesis)是金融學上的一個假說,認為股票市場的價格,會形成 隨機漫步模式,因此它是無法被預測的。它源自於效率市場假說。它認為,如果股市具有弱式有效性(Weak form efficiency),那么股票價格的變化服從隨機漫步 :
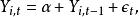 隨機漫步
隨機漫步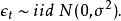 隨機漫步
隨機漫步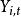 隨機漫步
隨機漫步1) 是 t時刻 i股票價格的自然對數,
 隨機漫步
隨機漫步2) 是常數,
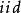 隨機漫步
隨機漫步3) :獨立同分布,
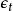 隨機漫步
隨機漫步4) 是誤差項。
