研究方法
隨機振動通常要用機率論的方法描述。機率反映隨機事件出現可能性的大小。將隨機事件的結果用數量描述，就得出隨機變數的概念，因為它描述隨機變數的發展過程，故又稱隨機過程，而隨機振動只是隨機過程的一類實例。
假設在一定條件下重複某個隨機試驗（如汽車道路試驗），得到系統回響（如司機座的鉛垂加速度）的一系列時變歷程記錄（見圖）。其中每個記錄
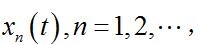隨機振動都可看作一個樣本，而大量樣本構成一個集合，記為X（t），用它代表這一隨機過程。
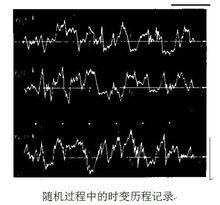
對於隨機現象，人們感興趣的往往不是各個樣本本身，而是從這些樣本總體得出的統計特性。例如，以隨機函式X在瞬時 t取值不大於 x的機率，可定義一維機率分布函式：
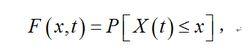隨機振動
隨機振動並由此導出一維機率密度函式：
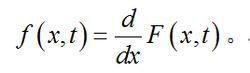隨機振動類似地，可定義多維機率分布與密度函式。從隨機函式的機率密度函式又可確定各種數字特徵；例如，各次矩可以定義如下：
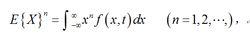隨機振動記號E{ }表述集合平均。可以看出，一次矩即隨機函式的平均值
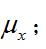隨機振動二次矩即均方值
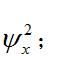隨機振動而二次中心矩
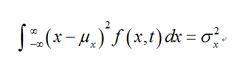隨機振動稱為方差，它的平方根
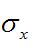隨機振動常稱為標準差。平均值反映過程的總傾向；均方值往往與平均能量相聯繫；方差則可用來表征隨機變數分散程度。
平均特性可區分為集合平均和時間平均。前者是對集合求平均，後者是對單個樣本來求的。根據統計特性是否隨採樣時間原點的選取而變化，隨機過程可分為非平穩過程和平穩過程。根據集合平均特性是否等同於時間平均特性，隨機過程又可分為遍歷的和非遍歷的。遍歷的隨機過程一定是平穩的；反之則不一定。
在各種平均特性中，最重要的是相關函式和功率譜密度。一個隨機振動又可以看作大量數目的具有隨機振幅與相位的諧和振動之和。它的總功率就等於各個諧和分量的功率之和。人們感興趣的是找出這種功率如何按頻率分布。平穩隨機函式
X的自相關函式
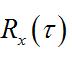隨機振動定義為乘積
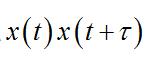隨機振動
隨機振動 隨機振動的集合平均值。它是時延的函式，反映相隔的的兩個時刻的隨機變數之間的線性相關程度，同時它還蘊藏著隨機過程中各個諧和分量的頻率和平均功率的信息。因此，從自相關函式的諧和變換
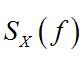隨機振動可得到功率譜密度（簡稱自譜）的機率，它恰好描述隨即過程的平均功率按頻率的分布規律。按定義有：
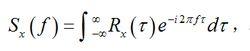隨機振動由逆諧和變換，得：
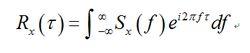隨機振動 隨機振動當=0時，
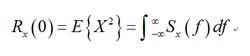隨機振動由此可見，
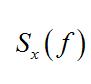隨機振動正是X關於頻率f的均方譜密度.
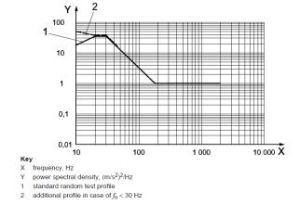
實用上，常用功率譜的形狀作為隨機過程的標誌，例如在隨機振動試驗中，各種基準譜都是按譜形來規定的。人們按譜形將偏於兩個極端的情況分為稱為窄帶過程和寬頻過程。窄帶過程是指它的功率譜具有尖峰特性，並只有在尖峰附近的一個窄帶內才取有意義的量級。典型的例子是隨機信號通過窄帶濾波器後所得的結果。相反地，寬頻過程的功率譜在相當寬（頻寬至少與其中心頻率有相同的數量級）的頻帶上取有意義的量級。最極端的情形是白噪聲，它的譜密度是均勻的並有無限的頻寬。白噪聲只是一種數學抽象，因為在無限的頻寬上都有有限的功率意味著有無限的總功率。不過，當隨機激勵的頻帶足夠寬，以致將系統所有的固有頻率覆蓋無遺時，把該激勵視為白噪聲是可取得，這樣做數學上便於處理。
自相關和自譜是從同一個隨機過程得到的統計特性，類似地可以定義兩個不同隨機過程X和Y之間的互相關函式
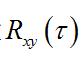隨機振動與互譜
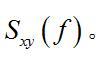隨機振動從互譜還可定義相干函式：
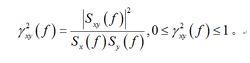隨機振動互譜和相干函式在實驗確定系統頻率特性以及確定振源和振動傳遞路徑方面有獨特的作用。
隨機過程中的一類特別重要的過程，稱為正態過程，亦稱高斯過程。平穩正態過程的一維機率密度函式可表示為：
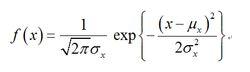隨機振動正態過程有以下特點：許多自然現象可以用正態過程近似地描述；正態過程的線性變換仍然是正態過程；只需知道正態過程的一次鉅與二次鉅，就可確定機率密度。這些特點給隨機振動研究帶來很大方便。首先，隨機振動的許多激振源（如大氣湍流、海浪、路面等）都可以看作正態過程。其次，從第二點可知，對於常係數線性系統，當輸入是正態過程，輸出也一定是正態過程，只要確定它們的平均值和方差，就可確定它們的全部統計特性。
研究內容
主要有以下兩方面：
①激勵-回響關係 前已提及，隨機振動問題中的激勵-回響關係只能描述為它們的統計特性之間的關係。常係數線性系統在平穩隨機激勵X作用下，產生平穩隨機回響Y。這時，關於平均值有如下關係：
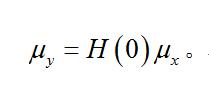隨機振動關於功率譜，有如下關係：
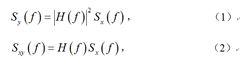隨機振動式中
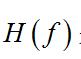隨機振動是系統的頻率特性。上述關係式既簡單又實用，這正是功率譜法的優點鎖在。式（1）只用到系統的幅頻特性，適用於已知系統特性，從輸入（或輸出）求輸出（或輸入）。式（2）適用於從實驗確定頻率的特性。功率譜雖然只提供了隨機過程的頻域描述，但知道功率譜後，就不難求出相關函式與均方值。如果輸入是平均值為零的正態過程，則輸出也一樣。這時，輸出的均方值也就完全確定了輸出的統計特性。
②可靠性 在系統可靠性分析中用到的隨機回響統計特性還有越界機率和峰值分布。越界機率是指隨機回響穿越某個界限水平次數的機率，峰值分布是指回響超越某個水平的峰數（或谷數）的機率。計算這些機率還需要知道隨機回響過程及其導數的聯合機率分布。
參考文獻
1、詞條作者：陳濱．《中國大百科全書》74卷（第一版）力學 詞條：隨機振動：中國大百科全書出版社，1987 ：455-456頁．
