定義
在機率論中, 隨機元是將隨機變數概念推廣到比簡單實線更複雜的空間概念。這個概念是由MauriceFréchet (1948)提出的,他評論說:“機率論的發展和其套用領域的擴展導致必須通過實驗的(隨機)結果可以用數字或有限集合描述的方案的數字,以實驗結果為代表的方案,例如矢量,函式,過程,場,系列,變換等集合“。
隨機元(random element)由機率空間到一個可測空間的映射 。
 隨機元
隨機元 隨機元
隨機元 隨機元
隨機元 隨機元
隨機元設一個機率空間{ Ω,F,P},和 一個可測量的空間。甲 隨機元素與值 ê是一個函式 X:Ω→ È這是 --可衡量。也就是說,任何一個函式都是這樣的 的前兆在於 。
 隨機元
隨機元有時隨機元素的值叫做評估隨機變數。
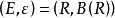 隨機元
隨機元 隨機元
隨機元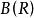 隨機元
隨機元注意如果,在哪裡是真實的數字,而且是它的Borelσ-代數,那么隨機元的定義就是隨機變數的經典定義。
隨機元素的定義
 隨機元
隨機元 隨機元
隨機元 隨機元
隨機元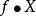 隨機元
隨機元 隨機元
隨機元在Banach空間中的值通常被理解為利用最小的上的所有有界線性泛函都是可測的。在這種情況下,等同於上述的定義是映射X:Ω→ B.從機率空間,如果是一個隨機元素是每個有界線性泛函 f的一個隨機變數,或者等價地說是弱可衡量的 。
隨機元的例子
1.隨機變數
隨機變數是最簡單的隨機元。表示一組映射X:Ω→ R是一組可能的結果中可衡量的功能Ω至 R。
作為一個實值函式,X經常描述給定事件的一些數字量。例如一定數量的硬幣翻轉後的頭數;不同的人的高度。
當圖像(或範圍)的X是有限的或無限的,隨機變數被稱為離散隨機變數,其分布可以用機率質量函式來描述,該機率質量函式將機率分配給圖像中的每個值X。如果圖像是無數的無限然後X被稱為連續隨機變數。在於它是特殊情況絕對連續,其分布可以通過進行說明機率密度函式,其分配機率區間;特別是對於絕對連續的隨機變數,每個單獨的點必然具有機率零。不是所有的連續隨機變數是絕對連續的,例如一個混合分布。這種隨機變數不能用機率密度或機率質量函式來描述。
2.隨機矢量
 隨機元
隨機元 隨機元
隨機元 隨機元
隨機元隨機向量是一個列向量(或其轉置,這是一個行向量),其是矢量隨機元。在相同機率空間{ Ω,F,P},在 Ω是樣本空間,是西格瑪代數(所有事件的集合),是機率測度(一個函式返回每個事件的機率)。
隨機向量經常被用作各種類型的聚合隨機變數的基礎實現,例如隨機矩陣,隨機樹,隨機序列,隨機過程等。
3.隨機矩陣
隨機矩陣是一個矩陣隨機元。物理系統的許多重要屬性可以在數學上表示為矩陣問題。例如,熱導率a的晶格可以從晶格內的顆粒與顆粒相互作用的動力學矩陣來計算。
4.隨機函式
隨機函式是一種隨機元,其中從某個函式族中選擇一個單一的結果,其中該族包括從域到共域的所有映射的一些類。例如,這個類可能被限制在所有的連續函式或者所有的步驟函式中。由同一實現的不同點評估的隨機函式所確定的值通常不會在統計上獨立,但取決於模型,在與不同實現相同或不同的點處確定的值可能被視為獨立。
5.隨機過程
隨機過程是一種集合隨機元,表示隨機值的一些系統隨時間演變。這是確定性過程(或確定性系統)的機率對應。而不是描述一個只能以一種方式進化的過程(例如一個常微分方程解的情況),在隨機或隨機過程中存在一些不確定性:即使初始條件(或起點)是已知的,有幾個(通常是無限多的)過程可能發展的方向 。
在離散時間情況下,與連續時間相反,隨機過程包含一系列隨機變數和與這些隨機變數相關的時間序列(例如,參見馬爾可夫鏈,也稱為離散時間馬爾可夫鏈)。
隨機幾何對象
這些包括隨機點,隨機數字和隨機形狀。
