簡介
陳省身類是復向量叢的一種上同調類。
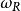 陳省身類
陳省身類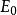 陳省身類
陳省身類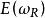 陳省身類
陳省身類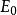 陳省身類
陳省身類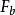 陳省身類
陳省身類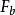 陳省身類
陳省身類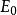 陳省身類
陳省身類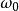 陳省身類
陳省身類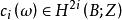 陳省身類
陳省身類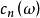 陳省身類
陳省身類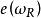 陳省身類
陳省身類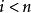 陳省身類
陳省身類設ω為復 n 維向量叢,為其基本實向量叢,表中所有非零向量所成子空間,中任意點 v 位於ω 的一個確定的纖維中,設ω 上給定埃爾米特度量,取 v 在中的正交補作為點 v 上的纖維,得以為底空間的復 n-1 維向量叢,則陳類按ω 的復維數遞推地定義為:頂陳類(即最高維陳類)等於歐拉類;對,定義為
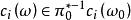 陳省身類
陳省身類 陳省身類
陳省身類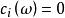 陳省身類
陳省身類對,類。
意義
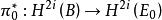 陳省身類
陳省身類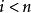 陳省身類
陳省身類陳省身類的定義是有意義的,因為在古津序列中,對於是一個同構。
乘積公式
若ω與是仿緊底空間B上的兩個復向量叢,則惠特尼ω⨁的全陳類有下述公式:c(ω⨁)=c(ω)·c(),這被稱為陳類的乘積公式。
