數學定義
函式 f的梅林變換是：
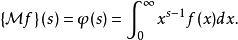Mellin變換逆變換是 ：
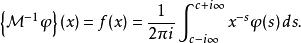Mellin變換這是在複平面上的垂直線上的線積分。在Mellin反演定理中給出了這種反演有效的條件。這個轉換以芬蘭數學家Hjalmar Mellin命名。
與其他變換的關係
雙邊拉普拉斯變換可以通過梅林變換來定義：
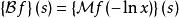Mellin變換相反，我們可以從雙邊拉普拉斯變換中得到梅林變換：
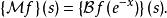Mellin變換我們也可以用梅林變換定義傅立葉變換，反之亦然。就梅林變換和上面定義的雙邊拉普拉斯變換而言：
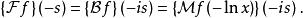Mellin變換反過來我們也可獲得：
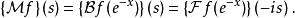Mellin變換梅林變換還通過泊松 - 梅林 - 牛頓循環將牛頓級數或二項式變換與泊松生成函式連線在一起。梅林變換也可以看作是Gelfand變換的卷積代數的局部緊湊阿貝爾正實數乘法。
Cahen-Mellin積分
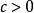Mellin變換
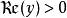Mellin變換
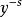Mellin變換對於 ， 和 在主要分支，一個
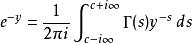Mellin變換
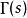Mellin變換其中 是伽馬函式。這個積分被稱為Cahen-Mellin積分。
數論
數論中的一個重要套用是簡單的函式 ：
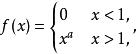Mellin變換
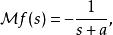Mellin變換
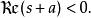Mellin變換因此， 假設
在機率論中
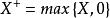Mellin變換
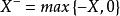Mellin變換在機率論中，梅林變換是研究隨機變數乘積分布的必要工具。如果 X是一個隨機變數，和 表示其正面部分，而 是其負部分，則梅林變換的 X被定義為：
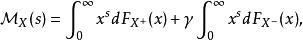Mellin變換
Mellin變換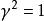
Mellin變換其中 滿足 。
機率論的梅林變換的重要性在於，如果X和Y是兩個獨立的隨機變數，然後X、Y的梅林變換的結果是X和Y的梅林變換的乘積 ：
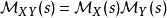Mellin變換套用
梅林變換由於其尺度不變性而被廣泛用於計算機科學分析算法。縮放函式的Mellin變換的幅度與純虛數輸入的原始函式的幅度相同。這種尺度不變性屬性類似於傅立葉變換的平移不變性。時移函式的傅立葉變換的幅度與原函式的傅立葉變換的幅度相同。
這個屬性在圖像識別中很有用。當物體朝向或遠離相機移動時，物體的圖像很容易被縮放。
在量子力學尤其是量子場論中，傅立葉空間是非常有用的，並且由於動量和位置是彼此的傅立葉變換（例如，在動量空間中更容易計算費曼圖），所以被廣泛使用。2011年，A. Liam Fitzpatrick，Jared Kaplan，JoãoPenedones，Suvrat Raju和Balt C. van Rees證明Mellin空間在AdS / CFT通信中起著類似的作用。
