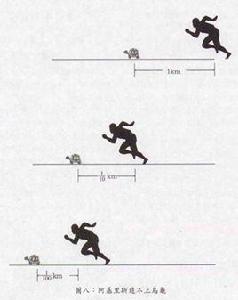
悖論解釋
關於阿基里斯悖論的一個解釋是:阿基里斯的確永遠也追不上烏龜。雖然現實中我們知道阿基里斯超越烏龜非常簡單,但是它是如何超過烏龜的在過去卻一直存在爭論。
現代物理學已經證明了時間和空間不是可以無限分割的,所以總有最為微小的一個時間裡,阿基里斯和烏龜共同前進了一個空間單位,從此阿基里斯順利超過烏龜。
產生原因
芝諾悖論的產生原因,是在於“芝諾時”不可能度量阿基里斯追上烏龜後的現象。在芝諾時達到無限後,正常計時仍可以進行,只不過芝諾的“鍾”已經無法度量它們了。 這個悖論實際上是反映 時空並不是無限可分的,運動也不是連續的。
通俗一點講,我們都知道一條線是由無數個點組成的,但這個“無數個點”並不能說我們無法畫出一條線。也就是說就是芝諾偷換了概念,(1+0.1+0.01+……)t其實是一個有限的時間,但他認為這個時間是無限大的,只要時間超過(1+0.1+0.01+……)t 阿基里斯就追上了烏龜。
哲學辨析
阿基里斯悖論分離了運動與靜止,把運動絕對化,否定客觀標準。是相對主義詭辯論。
黑格爾在《小邏輯》中說:“辯證法切不可與單純的詭辯相混淆。詭辯的本質在於孤立起來看事物,把本身片面的、抽象的規定,認為是可靠的。”辯證唯物主義認為,運動與靜止是對立統一的辯證關係。
一方面,運動與靜止的對立表現在:運動是絕對的,靜止是相對的,二者相互區別,不可混淆。所謂運動是絕對的是說,運動是物質的根本屬性,任何事物在任何條件下都是永恆運動的,是無條件的。所謂靜止是相對的是說,靜止是運動在特定條件下的特殊狀態,是有條件的。
另一方面,運動與靜止的統一表現在:運動和靜止是相互依存、相互貫通的,即所謂動中有靜、靜中有動。在運動與靜止關係上有兩種形上學的錯誤:一種是割裂運動與靜止的關係,否認運動,只講靜止,將靜止絕對化的形上學不動論;一種是割裂運動與靜止的關係,只講運動,否認靜止的形上學相對主義和詭辯論。
簡單證明
關於阿基里斯追龜的問題,我們可以很簡單地證明阿基里斯追上了烏龜。
我們設烏龜先前所走過的所有的點屬於集合B,烏龜現在所在的點標誌為b,烏龜所走過的所有的點是集合A,A由集合B中所有的點加上b點構成。只要是烏龜先前所在的點,都是阿基里斯可以走到的,因而阿基里斯可以走到集合B中所有的點。那么,我們能不能在集合A中找到一個點,它既不屬於B,也不是b,回答是不能的。因而如果阿基里斯走過了集合B中所有的點,阿基里斯與b點的距離就已經是0(如果不是0,則應該在阿基里斯與b點之間還會存在著一個點,但這個點並不存在),也就是說,阿基里斯已經追上了烏龜。
而按照我們悖論所設定的條件,阿基里斯是可以走到烏龜先前所走過的所有的點的。因而阿基里斯追到了烏龜。但在上面的分析中,我們發現了一個有趣的矛盾,這就是b既屬於B又不屬於B,也就是說,b既是現在又是先前。而且這是阿基里斯得以追上烏龜的前提和條件。這樣的一個有趣的結論,是決不可能為具有形上學頭腦的那些數學家們所接受的。
此悖論假設阿基里斯永遠只能到達龜前一個時間段到達的地方,即追上的前一個時間段,此時條件未發生變化,並先承認此時間段兩者間仍有差異,然後用不同的時間段進行重複換算,假設條件仍未變化。而在此時間段的下一個口徑相同的時間段里,阿基米斯就會追上。
相反觀點:這證明是錯誤的。因為證明假設了阿基里斯可以走一個點,在事實上迴避了悖論中無法找第1點問題實質。故此證明和悖論無關,只是把國小套用題用集合論複述了一遍。
推翻悖論
其實,我們根據中學所學過的無窮等比遞縮數列求和的知識,只需列一個方程就可以輕而易舉地推翻芝諾的悖論:阿基里斯在跑了
1000(1+0.1+0.01+…………)=1000 (1+1/9)=10000/9米時便可趕上烏龜。
人們認為數列1+0.1+0.01+…………是永遠也不能窮盡的。這只不過是一個錯覺。
我們不妨來計算一下阿基里斯能夠追上烏龜的時間為 t(1+0.1+0.01+…………)= t (1+1/9)=10t/9
芝諾所說的阿基里斯不可能追上烏龜,就隱藏著時間必須小於10t/9這樣一個條件。
由於阿基里斯和烏龜是在不斷地運動的,對時間是沒有限制的,時間很容易突破10t/9這樣一個條件。一旦突破10t/9這樣一個條件,阿基里斯就追上了或超過了烏龜。
人們被距離數列1+0.1+0.01+…………好像是永遠也不能窮盡的假象迷惑了,沒有考慮到時間數列1+0.1+0.01+…………是很容易達到和超過的了。
但是不是所有的數列都能達到,所以,我們看問題不能太極端。例如無論多少個點也不能組成直線,對於點的個數來說,我們就永遠無法窮盡它。
其實,以上的證明是無法推翻這個悖論的。因為這個證明用到了極限這個概念。然而,極限這個概念,正是為了解決阿基里斯悖論而定義出來的一個概念。用這個概念再反證這個悖論很明顯是不合理的。
無限的細分並不代表不會從時間1流入時間2,否則你的時鐘將永遠停留在59分59.9999............秒。
阿基里斯能夠繼續逼近烏龜,在某一時間點之前無法追上。但永遠追不上這一結果並不成立,因為這一悖論只引導去考慮追上之前的距離,而不是追上的這一距離。
悖論正解
悖論隱含的假設就是阿基里斯沒有追上龜,為什麼呢?阿基里斯的每一段,都是烏龜跑完了,才讓阿基里斯才跑的。只是想當然的用了一開始的距離差,而這個距離差為逐段變小。(是否能變成零,就是你說了算了)
而這個趨近過程又想用時間衡量,恰好時間和距離,都可以無限劃分。靜止也存在這樣的接近過程,舉個例子:假設烏龜是靜止的,讓阿基里斯以這樣的方式跑。900米,90米,9米,0.9米……,這樣他也追不上烏龜啊,也同樣變不成零,因為你的假設就是距離的無限小,這只是在尋找最短的距離。這個就關係到極限了。就像在找最小的物質粒子一樣。