基本解釋
凡陽曆中有閏日（二月為二十九日）的年，閏余（歲余置閏。陰曆每年與回歸年相比所差的時日）。
出處
宋·蘇軾 《監洞霄宮俞康直郎中所居四詠 退圃》：“園中草木春無數，只有黃楊厄閏年。”
宋·陸游 《蝸舍》詩：“麥因多雨損，蠶遇閏年遲。”
張生鏞1925年作《花卉圖》閏年開到十三回仿清·俞樾 《茶香室叢鈔·茨菰應閏月》：“茨菰一根，環十二子，閏年十三子。”
產生原因
通常的解釋是說一年有多少天多少小時多少分，取整數365還有多餘的，累積達到一天24小時後，就多加一天的年是閏年。這個解釋只是告訴了大家怎么計算，是人為設定的東西。
最根本的原因是：地球繞太陽運行周期為365天5小時48分46秒（合365.24219天）即一回歸年（tropical year）。公曆的平年只有365日，比回歸年短約0.2422 日，所餘下的時間約為每四年累計一天，故第四年於2月末加1天，使當年的歷年長度為366日，這一年就為閏年。現行公曆中每400年有97個閏年。按照每四年一個閏年計算，平均每年就要多算出0.0078天，這樣經過四百年就會多算出大約3天來。因此每四百年中要減少三個閏年。所以公曆規定：年份是整百數時，必須是400的倍數才是閏年；不是400的倍數的世紀年，即使是4的倍數也不是閏年。
這就是通常所說的：四年一閏，百年不閏，四百年再閏。 例如，2000年是閏年，2100年則是平年。
分類
閏年包括在公曆（格里曆）或夏曆中有閏日的年份，和在中國農曆中有閏月的年份。
公曆閏年
《中華民俗萬年曆》地球繞太陽運行周期為365天5小時48分46秒（合365.24219天），即一回歸年（ tropical year）。公曆的平年只有365日，比回歸年短約0.2422 日，每四年累積約一天，把這一天加於2月末（即2月29日），使當年時間長度變為366日（1-12月分別為31天，29天，31天，30天，31天，30天，31天，31天，30天，31天，30天，31天），這一年就為閏年。需要注意的是，公曆是根據羅馬人的“儒略曆”改編而 得。由於當時沒有了解到每年要多算出0.0078天的問題，從公元前46年，到16世紀，一共累計多出了10天。為此，當時的教皇格列高利十三世，將1582年10月5日人為規定為10月15日。並開始了新閏年規定。即規定公曆年份是整百數的，必須是400的倍數才是閏年，不是400的倍數的就是平年。比如，1700年、1800年和1900年為平年，2000年為閏年。此後，平均每年長度為365.2425天，約4年出現1天的偏差。按照每四年一個閏年計算，平均每年就要多算出0.0078天，經過四百年就會多出大約3天來，因此，每四百年中要減少三個閏年。閏年的計算，歸結起來就是通常說的：四年一閏；百年不閏，四百年再閏。
1950-2050年間的閏年：
1952、1956、1960、1964、1968、1972、1976、1980、1984、1988、1992、1996、2000、2004、2008、2012、2016、2020、2024、2028、2032、2036、2040、2044、2048。
由於地球的自轉速度逐漸降低，而公轉速度則相對更加穩定，所以上述的系統經過更長的周期也會發生微小的誤差。據計算，每8000年會有一天的誤差，所以英國的天文學家約翰·赫歇耳提議公元4000為平年，以後類推12000年，20000年亦為平年。但此提議從未被正式採納。原因是到了4000年，地球自轉的精確速度並非如今可以預測，所以屆時參照真實數據方可做出判斷。因此，在長遠的將來，針對閏年的微小調整應該不是由預定的系統決定，而是隨時不定性的。
農曆閏年
中國舊曆農曆作為陰陽曆的一種，每月的天數依照月虧而定，一年的時間以12個月為基準，平年比一回歸年少約11天。為了合上地球圍繞太陽運行周期即回歸年，每隔2到4年，增加一個月，增加的這個月為閏月。閏月加到哪個月，以農曆曆法規則推斷，主要依照與農曆的二十四節氣相符合來確定。在加有閏月的那一年有13個月，歷年長度為383至385日，這一年也稱為閏年。如1984年鼠年的農曆中，有兩個十月，通常稱為前十月和後十月（即閏月）。農曆閏年閏月的推算，3年一閏，5年二閏，19年七閏；農曆基本上19年為一周期對應於公曆同一時間。如公曆的2001年5月27日、1982年5月27日和1963年5月27日這個日子，都是閏四月初五。
超長農曆年
最長的農曆閏月年份的天數可長達385天，這樣的農曆閏月年份是很罕見的。從公元前221年至公元1900年的2120年裡，一共只有9次。從公元1900年至公元4000年這2100年裡出現了22次，出現的年份有：
1925年、1944年、2006年、2270年、2289年、2351年、2606年、2625年、2634年、2889年、2951年、2970年、3234年、3253年、3296年、3315年、3589年、3608年、3872年、3915年、3934年、3953年。
平年超短農曆年只有353天，公元元年至公元5000年之間，農曆年有353天的年份只有以下9個：
780年、1620年、1965年、2372年、3620年、3903年、3965年、4186年、4248年。
公曆1982年至2042年與農曆閏年閏月對照表：
| 1982年5月23日 閏四月小 壬戊年 | 2014年10月24日 閏九月小 甲午年 |
| 1984年11月23日 閏十月小 甲子年 | 2017年7月23日 閏六月大 丁酉年 |
| 1987年7月26日 閏六月小 丁卯年 | 2020年5月23日 閏四月小 庚子年 |
| 1990年6月23日 閏五月小 庚午年 | 2023年3月22日 閏二月小 癸卯年 |
| 1993年4月22日 閏三月小 癸酉年 | 2025年7月25日 閏六月小 乙巳年 |
| 1995年9月25日 閏八月小 乙亥年 | 2028年6月23日 閏五月小 戊申年 |
| 1998年6月24日 閏五月小 戊寅年 | 2031年4月22日 閏三月小 辛亥年 |
| 2001年5月23日 閏四月小 辛巳年 | 2033年8月25日 閏冬月小 癸丑年 |
| 2004年3月21日 閏二月小 甲申年 | 2036年7月23日 閏六月大 丙辰年 |
| 2006年8月24日 閏七月小 丙戊年 | 2039年6月22日 閏五月小 己未年 |
| 2009年6月23日 閏五月小 己丑年 | 2042年3月22日 閏二月小 壬戊年 |
| 2012年5月21日 閏四月小 壬辰年 |
判定方法
公曆閏年計算
（按一回歸年365天5小時48分45.5秒）
1、非整百年：能被4整除的為閏年。（如2004年就是閏年,2001年不是閏年）
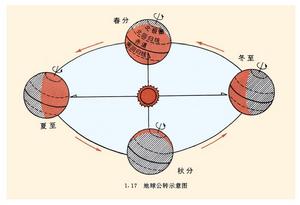地球公轉示意圖2、整百年：能被400整除的是閏年。(如2000年是閏年，1900年不是閏年)
3、對於數值很大的年份：這年如果能被3200整除，並且能被172800整除則是閏年。如172800年是閏年，86400年不是閏年（因為雖然能被3200整除，但不能被172800整除）（此按一回歸年365天5h48'45.5''計算）。
按一回歸年365天5h48'45.5''計算：3200年多出16000小時153600分145600秒 =18600小時26分40秒，現行公曆中每400年有97個閏年，3200年共97*8=776個閏年=776*24小時=18624小時 >18600小時，所以只能算到775個閏年，3200不是閏年，於是775*24=18600，多出了26分40秒（總計1600秒），怎么辦？需要經歷多少個3200年的周期，足夠彌補1天（86400秒）？答案是剛好54個周期（86400=1600*54），歷時172800（=3200*54）年。
公元前閏年計算
根據閏年算法，公元4年是閏年，且周期是4年，如果公元有0年，即為閏年。因為公元沒有0年，那公元前1年就是是閏年。
1、非整百年：年數除以4餘數為1是閏年，即公元前1、5、9……是閏年；
2、整百年：年數除以400餘數為1是閏年，即公元前401、801……是閏年；
3、對於數值很大的年份：年數除以3200餘數為1則不是閏年且年數除以172800餘1又為閏年，即公元前172801……是閏年，864001……年不是閏年。
128年31閏置閏法
這一規則曾在19世紀提出，但不知何故沒被兩教派採納。比起400年3不閏和900年7不閏的規則，128年31閏更精確更簡便。
按現行的閏年規則，從2052年到2096年間的閏年與回歸年的誤差都會超過一天以上，如採用128年31閏規則不會這么早出現這種情況。
128年31閏的置閏方案的優點和實施方法：
1、採用128年31閏的置閏的方法，可以大大地減少歷年與回歸年的誤差，回歸年長度是365.24219879日，128年31閏的平均年長是365.2421875日。歷年與回歸年的平均誤差每年不到一秒，是曆法與回歸年平均誤差的27分之一。
2、改歷後與現曆法銜接好，不須要過渡階段。其方法如下：現曆法繼續使用，到2048年停閏，以後每加128年既不閏。新曆法規則是：每四年一閏，凡公元年數能被128整除的年不閏。
3、此曆法非常科學，它的置閏方法比現曆法更簡單，更符合天體運行規律，現曆法平均每年與回歸年誤差26秒，而此曆法每年與回歸年平均誤差不到一秒。經計算，如果回歸年按如今長度計算，得八萬多年，新曆法與回歸年的誤差才能超過一日。而現曆法與回歸年的誤差3300年即超過一日。此曆法好記簡單，便於歷算，凡公元年數能被128整除的年不閏。
閏年計算
2017年經過研究，閏年的計算應該如下：
口訣1：4年1閏，400年97閏，3200年（97*8-1）閏，86400年（27*（97*8-1）+1）閏（20926閏）
口訣2：4年1閏，128年31閏，86400年（675*31+1）閏（20926閏）
*************************************
一個回歸年，H=（365*24*3600+5*3600+48*60+46）秒=31556926秒=15778463*2秒
1天 D=86400秒=43200*2秒
一個回歸年=H/D天=15778463*2/（43200*2）天=365.2421990740740740740740740740....天
4年一閏：365*4+1=1461天=15778800/10800天
4個回歸年為（15778463/43200）*4=15778463/10800天
4年一閏，公曆比回歸年時間多337/10800天
增加百年不閏400年再閏規則後：
400個公曆年天數為365*400+97=146097天=15778476/108天
400個回歸年為（15778463/43200）*400=15778463/108天
公曆比回歸年時間多13/108天
增加3200年不閏規則後：
3200個公曆年天數為365*3200+97*（3200/400）-1=1168775天=31556925/27天
3200個回歸年為15778463*3200/43200=15778463*32/432=31556926/27天
公曆比回歸年時間少1/27天
增加86400年再閏規則後：
86400個公曆年天數為365*86400+（97*8-1）*（86400/3200）+1=365*86400+775*27+1=31556926=852037002/27天
86400個回歸年為15778463*86400/43200=15778463*864/432=15778463*54/27=852037002/27天
公曆比回歸年時間少0天
結論：一天定義24小時即86400秒，需要86400年一個循環才能消除公曆和回歸年時間差。
*******************************
（365*24*3600+5*3600+48*60+46）=31556926秒（15778463*2）
1天=86400秒；（43200*2）
一個回歸年等於15778463/43200天=365.2421990740740740740740740740....天
4年一閏：365*4+1=1461天=15778800/10800天
4個回歸年為（15778463/43200）*4=15778463/10800天
4年一閏，公曆比回歸年時間多337/10800天
增加128年不閏後：
128個公曆年天數為365*128+128/4-1=46751天=31556925/675天
128個回歸年為（15778463/43200）*128=15778463*2/675天=31556926/675天
公曆比回歸年時間少1/675天
增加86400年再閏規則後：
86400個公曆年天數為365*86400+31*675+1=31556926天
86400個回歸年為15778463*86400/43200=15778463*2=31556926天
公曆比回歸年時間少0天
結論：一天定義24小時即86400秒，需要86400年一個循環才能消除公曆和回歸年時間差。
口訣：4年1閏，128年不閏，86400年再閏。
祖沖之
祖沖之改革曆法在古代，我國曆法家一向把十九年定為計算閏年的單位，稱為“一章”，在每一章里有七個閏年。也就是說，在十九個年頭中，要有七個年頭是十三個月。這種閏法一直採用了一千多年，不過它還不夠周密、精確。公元412年，北涼趙厞創作《元始歷》，才打破了歲章的限制，規定在六百年中間插入二百 二十一個閏月。可惜趙厞的改革沒有引起當時人的注意，例如著名歷算家何承天在公元443年製作《元嘉歷》時，還是採用十九年七閏的古法。
祖沖之吸取了趙厞的先進理論，加上他自己的觀察，認為十九年七閏的閏數過多，每二百年就要差一天，而趙厞六百年二百二十一閏的閏數卻又嫌稍稀，也不十分精密。因此，他提出了三百九十一年內一百四十四閏的新閏法，這個閏法在當時算是最精密的了。
除了改革閏法以外，祖沖之在曆法研究上的另一重大成就，是破天荒第一次套用了“歲差”。
”祖沖之在曆法研究方面的第三個巨大貢獻，就是能夠求出曆法中通常稱為“交點月”的日數。
祖沖之根據上述的研究成果，終於成功製成了當時最科學、最進步的曆法——《大明曆》。這是祖沖之科學研究的天才結晶，也是他在天文曆法上最卓越的貢獻。
計算方法
精確計算方法
（按一回歸年365天5小時48分45.5秒）
①、普通年能被4整除且不能被100整除的為閏年。（如2004年就是閏年，1900年不是閏年）
②、世紀年能被400整除的是閏年。（如2000年是閏年，1900年不是閏年）
③、對於數值很大的年份，這年如果能整除3200，並且能整除172800則是閏年。如172800年是閏年，86400年不是閏年（因為雖然能整除3200，但不能整除172800）（此按一回歸年365天5h48'45.5''計算）。
此外，如依照現有太陽年的長度與上述閏年規則，每8000年又約差一日，因此約翰·赫歇爾提議每逢4000的倍數不閏，如西元4000年。但距此一年份來臨尚有約二千年之遙，因此還未曾真正納入規則或實施過。又由於地球公轉速率的不穩定與眾多影響因素，屆時是否需要納入此規則仍有疑問。
原因：若一年按365天5h48'46''（此時86400年也是閏年）計算，一年日數必須是整數，不便將零時數計入，所以取365天為一年，則餘5時48分46秒 ，積至4年約滿一 日，所以4年一“閏日”，謂之“閏年”，無“閏日”之年為平年，即平年365天，閏年366天。但到4年之時，僅有23時15分4秒閏一日，欠缺44分56秒；積至100年（25閏）時就欠缺18時43分20秒，約合3 / 4日，所以滿100年不閏；此時又餘5時16分40秒，積至400年餘21時6分40秒又閏；又欠缺2時53分20秒，積至3200年計欠缺23時6分40秒，所以滿3200年不閏；此時又餘53分20秒，積至86400年剛好24 時又一閏，這是不余不欠，需重計算，所以按陽曆計算就有上面的閏年規則。
按一回歸年365天5h48'45.5''計算：3200年多出16000小時153600分145600秒 =18600小時26分40秒，現行公曆中每400年有97個閏年，3200年共97*8=776個閏年=776*24小時=18624小時 >18600小時，所以只能算到775個閏年，3200不是閏年，於是775*24=18600，多出了26分40秒怎么辦需要多少個周期彌補？答案是54個周期，為172800年，因為172800/3200=54個周期 54*26分40秒=1404分2160秒=24小時。
程式計算
Ecmascript語言：
C#語言:
Java語言：
VB語言：
Python 語言：
C++語言：
C語言：
MATLAB語言：
Erlang語言：
Bash/Shell：
易語言：
Go語言：
