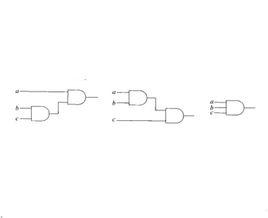
基本介紹
開關代數是二值代數,即所有的變數和常數隻取兩個值之一:0或1。不是自然二進制的量必須被編碼為二進制格式。在物理上,它們可以代表一個燈的開和關,一個開關的合和開,一個低電壓和一個高電壓,一個在一個方向或另一個方向的磁場。開關代數是邏輯代數的一種套用。研究由開關的並聯和串聯所構成的電路的通斷情況。以變元表示開關;數字0,1分別表示開關的斷開與接通;3種基本運算“-”、“∧”、“∨”(即: -,∩,∪)表示開關的基本連線方式:反相、串聯、並聯(反向可以用字母上加短橫線也可以用'表示)。用代數方法解決開關線路的分析和設計問題。在電子計算機、自動程式控制、電話交換系統中有廣泛套用。依據代數的觀點,是什麼物理意義無關緊要。在實驗室中,將選擇其中一種物理表象來表示其中一個值。
下面首先定義開關代數的三個運算符號,然後研究開關代數的若干性質 。
開關代數的三個運算符號
① 或 OR(記作+)
a+b(讀作a或b),若且唯若a=1或b=1或二者都為1時,它等於1
② 與AND(記作·或乾脆把兩個變數連寫)
a·b=ab(讀作a與b),若且唯若a=1並且b=1時,它等於1
③ 非 NOT(記作'或字母上加短橫線)
a'(讀作a非),若且唯若a=0時,它等於1。
術語反有時被用來代替非,其運算是指求反,實現它的器件經常被稱為反相器。
因為或的符號與普通代數中加的符號相同,與的符號與普通代數中乘的符號相同,所以一般用術語“和”和“積”。因此,ab經常指一個積項,a+b為一和項。下面討論的許多性質適用於普通代數,同時也適用於開關代數。但是,正像將要看到的,有一些明顯的例外 。
三種運算符的真值表如表1、2、3所示。
| + | 0 | 1 |
| 0 | 0 | 1 |
| 1 | 1 | 1 |
| · | 0 | 1 |
| 0 | 0 | 0 |
| 1 | 0 | 1 |
| a | a' |
| 0 | 1 |
| 1 | 0 |
開關代數的性質
現在來研究開關代數的一組性質(這些性質有時稱為定理)。
1.結合律:(a+b)+c=a+(b+c) ,
(a·b)·c=a·(b·c).
2.交換律:a+b=b+a, a·b=b·a.
3.分配律:a·(b+c)=(a·b)+(a·c),
a+(b·c)=(a+b)·(a+c).
4.吸收律:a+a·b=a, a·(a+b)=a.
5.冪等律:a+a=a, a·a=a.
6.德·摩根律(反演律):(a+b)′=a′·b′,
(a·b)′=a′+b′.
7.對合律(雙重否定律):(a′)′=a.
8.互補律:a+a′=1, a·a′=0.
9.零一律(麼元律):a+0=a, a·1=a.
10.囿元律(極元律):a+1=1, a·0=0.
門電路
構成開關電路的基本單元。每一種門電路的輸入與輸出之間,都有一定的邏輯關係。這裡邏輯是指“條件”與“結果”的關係。利用電路的輸入信號反映“條件”,而用電路的輸出反映“結果”,從而使電路的輸出、輸入之間代表了一定的邏輯關係。最基本的邏輯關係可以歸結為與、或、非三種。其他複雜的邏輯關係都是由這三種基本邏輯關係組合而成的,因此可以利用基本門電路(見與門、或門、非門、異或門)組成具有各種邏輯功能的數字電路。除基本門電路之外,常用的門電路還有與非、或非、與或非等門電路。所有門電路都有系列化積體電路產品供選用。
在邏輯電路中,存在著兩種相互對立的邏輯狀態,例如電位的“高”與“低”,脈衝的“有”與“無”,開關的“合”與“開”,事物的“真”與“假”等。通常用符號0和1表示兩種對立的邏輯狀態,稱為邏輯0和邏輯1。這樣就可選用各種僅具有兩種狀態的元件來組成各種邏輯功能的電路,如繼電器、開關、二極體和三極體、集成門電路等。
在邏輯電路中,有兩種邏輯體制:一種用1表示高電位,用0表示低電位,這就是“正邏輯體制”。另一種是用1表示低電位,用0表示高電位,這就是“負邏輯體制”。
對於同一電路,可以用正邏輯體制,也可以用負邏輯體制。根據所選用正負邏輯體制的不同,即使同一電路也具有不同的邏輯功能。
在邏輯電路中,電位的高、低常用高電平、低電平來描述,單位為V(伏)。由於溫度變化、電源電壓波動、干擾及元件特性變化等因素的影響,實際的高電平和低電平都不是一個固定數值,因此通常考慮一個電平變化範圍。如果電平在此範圍內,就判斷為1狀態或0狀態 。