簡介
商賦范線性空間是由賦范線性空間與其閉子空間誘導出的新的賦范線性空間。
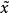 商賦范線性空間
商賦范線性空間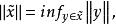 商賦范線性空間
商賦范線性空間設E是賦范線性空間(X,||·||)的閉線性子空間,對於商空間X/E中每個元,規定範數則X/E成為賦范線性空間,稱為商賦范線性空間,這個範數稱為原來範數的誘導範數。
性質
如果(X,||·||)是巴拿赫空間,則商空間X/E按誘導範數也是巴拿赫空間。
賦范線性空間
賦范線性空間(normed linear space)是線上性空間中引進一種與代數運算相聯繫的度量,即由向量範數誘導出的度量。賦范線性空間稱為Banach空間,是指由範數導出的度量是完備的。
 商賦范線性空間
商賦范線性空間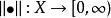 商賦范線性空間
商賦范線性空間 商賦范線性空間
商賦范線性空間定義:設是線性空間,函式稱為上定義的一個範數,如果滿足:
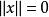 商賦范線性空間
商賦范線性空間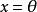 商賦范線性空間
商賦范線性空間(1)若且唯若;
 商賦范線性空間
商賦范線性空間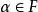 商賦范線性空間
商賦范線性空間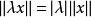 商賦范線性空間
商賦范線性空間(2)對任何及,;
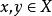 商賦范線性空間
商賦范線性空間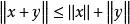 商賦范線性空間
商賦范線性空間(3)對任意,。
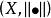 商賦范線性空間
商賦范線性空間稱二元體為賦范線性空間。
