在分子體系內部,化學鍵都有“自然”的鍵長值和鍵角值。分子要調整它的幾何形狀(構象),以使其鍵長值和鍵角值儘可能接近自然值,同時也使非鍵作用(van der Waals力)處於最小的狀態,給出原子核位置的最佳排布。因此需要一個物理量來衡量體系內的原子分布是不是符合“自然狀態”,這個物理量就是所謂的勢能(Potential Energy ),因在哈密頓(Hamiltonian)表述中,勢能習慣寫為V,與電勢V相同,因此也可由potential代指。
Bohm和Hiley對於量子勢能的概念詮釋導致物理學家開始注意到量子物理中最基本的新性質─非局域性(nonlocality)。
勢能越高體系往往越不穩定,因為攜帶了更多可以轉化的潛力。量子力學裡的能量守恆是平均值守恆,能量平均值=動能平均值+勢能平均值勢能是分子體系中各種能量的總和,雖然相比於彈性勢能和重力勢能,分子體系的勢能的組分更複雜,可以分成兩大類:共價鍵勢能和非共價相互作用能。
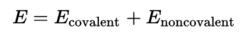 量子勢能
量子勢能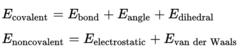 量子勢能
量子勢能勢能只和原子間的相對坐標及原子帶有的局部電荷相關。通過對勢能函式的計算和最佳化,可以獲得分子體系內各個原子之間處在什麼樣的相對坐標分布的情況下勢能最低,這就是所謂的分子的低能構象或優勢構象。
套用領域
量子勢能的方法可被用在量子效應的建模(modeling)上,不需明確地解出薛丁格方程。量子勢能也可與蒙特卡洛(Monte Carlo method)模擬結合,模擬可用於(深)次微米元件的載子傳輸問題,如載子流體力學方程(Hydrodynamic, HD,此處指元件載子傳輸現象的動力方程,與流體無關,僅因描述公式的型式與傳統流體力學相似而得名 )和擴散方程。此計算方法先決定各個流體元素(fluid element)的密度,接著流體元素的加速經由計算V和Q的梯度得出,最後速度場的散度決定密度的變化。在商用的元件模擬軟體,如SILVACO TCAD,已可加入量子勢能來模擬元件行為。
套用實例
薛丁格方程中的量子勢能。
薛丁格總方程式為:
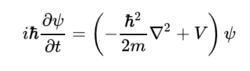 量子勢能
量子勢能可由含有實函式R和S的極坐標型式的波函式ψ改寫。其中R和S分別為波函式的振幅和相位。改寫後可將方程寫成兩個部分,分別對應到實部和虛部,實部部分稱為量子哈密頓-亞克比方程(Hamilton-Jacobi equation),虛部部分稱為連續方程。
薛丁格方程虛部部分的連續方程
1.薛丁格方程虛部部分的連續方程
表達式:
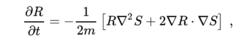 量子勢能
量子勢能如果ρ=R square,上式可變形為連續方程:
∂ρ/∂t+▽*(ρv) = 0
2. 薛丁格方程實部部分的量子哈密頓-亞克比方程
表達式:
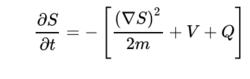 量子勢能
量子勢能量子哈密頓-亞克比方程與經典哈密頓-亞克比方程多出一項,如下所示:
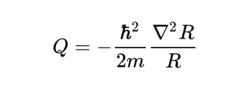 量子勢能
量子勢能其中,Q即為量子勢能。該公式表示,量子勢能與波函式振幅的曲率(curvature)有關。取極限為0時,函式h為經典哈密頓-亞可比方程的解,因此函式S又可稱為哈密頓-亞可比函式,或者是可延伸至量子物理的作用量(action)。
總能,勢能,動能之間的關係
量子力學中,能量是總稱動能,勢能,機械能,熱能等都是能量的一種。
能量包含動能和勢能,動能+勢能=機械能(外在能量)+熱能(物體內在能量)=物體的能量

