一維諧振子
哈密頓算符與能量本徵態
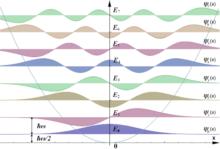 圖1.能量最低的六個束縛本徵態的波函式表征
圖1.能量最低的六個束縛本徵態的波函式表征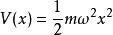 量子諧振子
量子諧振子在一維諧振子問題中,一個質量為 m的粒子,受到一位勢。此粒子的哈密頓算符為
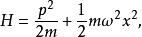 量子諧振子
量子諧振子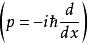 量子諧振子
量子諧振子其中 x為位置算符,而 p為動量算符。第一項代表粒子動能,而第二項代表粒子處在其中的勢能。為了要找到能階以相對應的能量本徵態,必須解所謂的“定態薛丁格方程”:
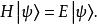 量子諧振子
量子諧振子在坐標基底下可以解這個微分方程,用到冪級數方法。可以見到有一族的解:
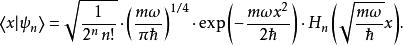 量子諧振子
量子諧振子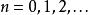 量子諧振子
量子諧振子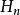 量子諧振子
量子諧振子最先六個解( n= 0到5)展示在右圖。函式為埃爾米特多項式:
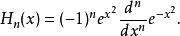 量子諧振子
量子諧振子注意到不應將之與哈密頓算符搞混,儘管哈密頓算符也標作 H。相應的能階為
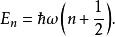 量子諧振子
量子諧振子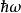 量子諧振子
量子諧振子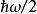 量子諧振子
量子諧振子值得注意的是能譜,理由有三。首先,能量被“量子化”(quantized),而只能有離散的值——即乘以1/2, 3/2, 5/2……等等。這是許多量子力學系統的特徵。在爾後的“階梯算符”段落,將對此現象做更詳細的檢視。再者,可有的最低能量(當 n= 0)不為零,而是,被稱為“基態能量”或零點能量。在基態中,根據量子力學,一振子執行所謂的“零振動”(null oscillations)且其平均動能是正值。這樣的現象意義重大但並不那么顯而易見,因為通常能量的零點並非一個有意義的物理量,因為可以任意選擇;有意義的是能量差。雖然如此,基態能量有許多的意涵,特別是在量子引力。最後一個理由式能階值是等距的,不像玻爾模型或盒中粒子問題那樣。
注意到基態的機率密度集中在原點。這表示粒子多數時間處在勢阱的底部,合乎對於一幾乎不帶能量之狀態的預期。當能量增加時,機率密度變成集中在“經典轉向點”(classical turning points),其中狀態能量等同於勢能。這樣的結果與經典諧振子相一致;經典的描述下,粒子多數時間處在(而更有機會被發現在)轉向點,因為在此處粒子速度最慢。因此滿足對應原理。
階梯算符方法
前述的冪級數解雖然直觀,但顯得相當繁複。階梯算符方法起自保羅·狄拉克,允許抽像求得能量本徵值,而不用直接解微分方程。此外,此法很容易推廣到更複雜的問題,尤其是在量子場論中。跟從此方法,定義算符 a與其伴隨算符(adjoint) a:
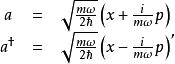 量子諧振子
量子諧振子算符 a並非厄米算符(Hermitian),以其與伴隨算符 a並不相同。
算符 a與 a有如下性質:
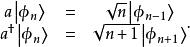 量子諧振子
量子諧振子在推導 a形式的過程中,已用到算符 x與 p(代表可觀測量)為厄米算符這樣的事實。這些可觀測量算符可以被表示為階梯算符的線性組合:
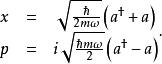 量子諧振子
量子諧振子x與 p算符遵守下面的等式,稱之為正則對易關係:
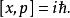 量子諧振子
量子諧振子方程中的方括弧是常用的標記機器,稱為交換子、 交換算符或 對易算符,其定義為
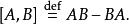 量子諧振子
量子諧振子利用上面關係,可以證明如下等式:
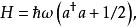 量子諧振子
量子諧振子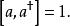 量子諧振子
量子諧振子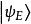 量子諧振子
量子諧振子現在,讓代表帶有能量 E的能量本徵態。任何右括矢量(ket)與自身的內積必須是非負值,因此
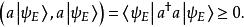 量子諧振子
量子諧振子將 a a以哈密頓算符表示:
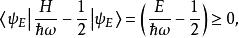 量子諧振子
量子諧振子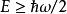 量子諧振子
量子諧振子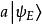 量子諧振子
量子諧振子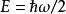 量子諧振子
量子諧振子因此。注意到當()為零右括矢量(亦即:長度為零的右括矢量),則不等式飽和而。很直觀地,可以檢查到存在有一狀態滿足此條件——前面段落所提到的基態( n= 0)。
利用上面等式,可以指出 a及 a與 H的對易關係:
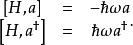 量子諧振子
量子諧振子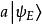 量子諧振子
量子諧振子因此要是()並非零右括矢量,
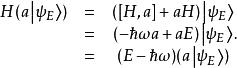 量子諧振子
量子諧振子類似地,也可以指出
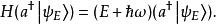 量子諧振子
量子諧振子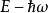 量子諧振子
量子諧振子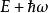 量子諧振子
量子諧振子換句話說, a作用在能量為 E的本徵態,而產生出——還多了一個常數乘積——另一個能量為的本徵態,而 a作用在能量為 E的本徵態,產生出另一個能量為的本徵態。因為這樣, a稱作降算符而 a稱作升算符。兩者合稱階梯算符。在量子場論中, a與 a也分別稱作消滅算符與創生算符,以其分別摧毀與創造粒子——對應於能量量子。
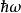 量子諧振子
量子諧振子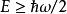 量子諧振子
量子諧振子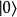 量子諧振子
量子諧振子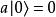 量子諧振子
量子諧振子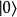 量子諧振子
量子諧振子給定任何能量本徵態,可以拿降算符 a作用在其上,產生了另一個能量少了的本徵態。重複使用降算符,似乎可以產生能量本徵態其能量低到 E= −∞。不過這樣就就與早先的要求相違背。因此,必須有一最底的能量本徵態——基態,標示作(勿與零右括矢量混淆),使得(即 a對作用後產生零右括矢量(zero ket))。
在這情況下,繼續使用降算符只會產生零右括矢量,而不是產生額外的能量本徵態。此外,還指出了
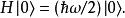 量子諧振子
量子諧振子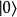 量子諧振子
量子諧振子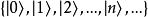 量子諧振子
量子諧振子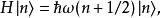 量子諧振子
量子諧振子最後,透過將升算符作用在上,並且乘上適當的歸一化因子,可以產生出一個能量本徵態的無限集合使得這與前段所給的能譜相符合。
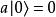 量子諧振子
量子諧振子這方法也能夠用來很快地找到量子諧振子的基態波函式。只要將消滅算符作用於基態,變為
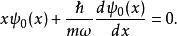 量子諧振子
量子諧振子所以
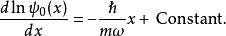 量子諧振子
量子諧振子這個方程的解為,經過歸一化,
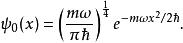 量子諧振子
量子諧振子自然長度與能量尺度
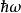 量子諧振子
量子諧振子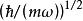 量子諧振子
量子諧振子量子諧振子擁有自然長度與自然能量兩個自然尺度,可以用來簡化問題。這可以透過無量綱化來得到。結果是如果以為單位來測量能量,以及為單位來測量距離,則薛丁格方程變成:
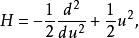 量子諧振子
量子諧振子且能量本徵態與本徵值變成
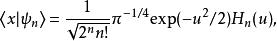 量子諧振子
量子諧振子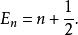 量子諧振子
量子諧振子為了避免混淆,在此文中不採用這些自然單位。不過,這用法在執行運算上總會因便利性而遲早被使用。
案例:雙原子分子
主條目:雙原子分子
在雙原子分子中,自然頻率可以發現為:
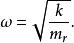 量子諧振子
量子諧振子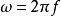 量子諧振子
量子諧振子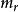 量子諧振子
量子諧振子其中為角頻率, k是 共價鍵勁度係數,是約化質量。
N維諧振子
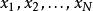 量子諧振子
量子諧振子一維諧振子很容易地推廣到N維。在一維中,粒子的位置是由單一坐標 x來指定的。在N維中,這由N個位置坐標所取代,以標示。對應每個位置坐標有個動量,標示為 p, ..., p。這些算符之間的正則對易關係為
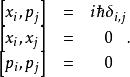 量子諧振子
量子諧振子系統的哈密頓算符為
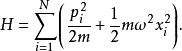 量子諧振子
量子諧振子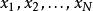 量子諧振子
量子諧振子從這個哈密頓量的形式,可以發覺,N維諧振子明確地可比擬為N個質量相同,彈性常數相同,獨立的一維諧振子。在這案例里,變數是N個粒子的位置坐標。這是反平方連心位勢的一個優良的特性,允許位勢被分離為N個項目,每一個項目只跟一個位置坐標有關。
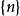 量子諧振子
量子諧振子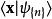 量子諧振子
量子諧振子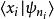 量子諧振子
量子諧振子這觀察使得問題的解答變的相當簡單。對於一個集合的量子數,一個N維諧振子的能量本徵函式等於N個一維本徵函式的乘積:
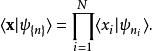 量子諧振子
量子諧振子採用階梯算符方法,定義N組階梯算符:
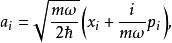 量子諧振子
量子諧振子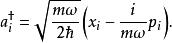 量子諧振子
量子諧振子 量子諧振子
量子諧振子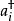 量子諧振子
量子諧振子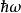 量子諧振子
量子諧振子類似前面所述的一維諧振子案例,可以證明每一個與算符將能量分別降低或升高。哈密頓量是
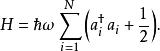 量子諧振子
量子諧振子這量子系統的能階E是
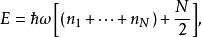 量子諧振子
量子諧振子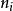 量子諧振子
量子諧振子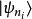 量子諧振子
量子諧振子其中,正整數是的量子數。
如同一維案例,能量是量子化的。N維基態能階是一維基態能階的N倍。只有一點不同,在一維案例里,每一個能階對應於一個單獨的量子態。在N維案例里,除了底態能階以外,每一個能階都是簡併的,都對應於多個量子態。
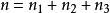 量子諧振子
量子諧振子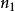 量子諧振子
量子諧振子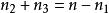 量子諧振子
量子諧振子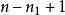 量子諧振子
量子諧振子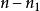 量子諧振子
量子諧振子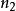 量子諧振子
量子諧振子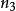 量子諧振子
量子諧振子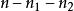 量子諧振子
量子諧振子簡併度可以很容易地計算出來。例如,思考三維案例,設定。每一個N相同的量子態,都會擁有相同的能量。給予N,首先選擇一個。那么,,有個值,從0到,可以選擇為的值。的值自動的設定為。因此,簡併度是
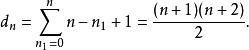 量子諧振子
量子諧振子對於N維案例,
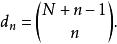 量子諧振子
量子諧振子耦合諧振子
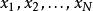 量子諧振子
量子諧振子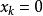 量子諧振子
量子諧振子構想N個相同質量的質點,以彈簧連結為一條一維的線形鏈條。標記每一個質點的離開其平衡點的位置為(也就是說,假若一個質點k位於其平衡點,則)。整個系統的哈密頓量是
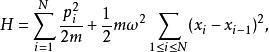 量子諧振子
量子諧振子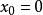 量子諧振子
量子諧振子其中,。
很奇妙地,這個問題可以用坐標變換來變換成一組獨立的諧振子,每一個獨立的諧振子對應於一個獨特的晶格集體波震動。這些波震動表現出類似粒子般的性質,稱為聲子。許多固體的離子晶格都會產生聲子。在固體物理學裡,這方面的理論對於許多現象的研究與了解是非常重要的。
參閱
•自由粒子
•無限深方形阱
•有限深方形阱
•有限位勢壘
•球對稱位勢
•Delta位勢壘
