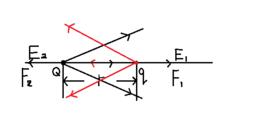
動力學對稱性和庫侖簡併
【摘要】:在量子力學中,束縛態能級常出現簡併現象,理論指出,簡併起源於體系的對稱性。庫侖場中的束縛電子(E<O),由空間旋轉對稱性引起的簡併有(2i+1)重簡併(本文忽略自旋)這是一種幾何時稱性,在標誌這種對稱性的算符作用下,不改變體系的勢能,而實際簡併有重簡併,這說明體系除具有旋轉對稱性外,還有新的對稱性。本文指出,這是一種動力學對稱性,是體系內部的對稱性。在這種算符作用下,使勢能和動能同時改變,而哈密頓整體保持不變,一般稱為庫侖對稱性,由此引起的簡併稱為庫侖簡併。
用克萊因-戈登方程推導兩質子之間的庫侖勢
【摘要】:量子電動力學認為庫侖力是電荷之間交換虛光子的結果,最有力的證據是從虛光子假說直接推出庫侖勢能.克萊因-戈登方程(□2-m2)Φ(x,t)=0是一個用來描述質量為m,自旋為0,電荷為0的標量場的場方程,虛光子可以用粒子靜止質量為0的標量場描述,因此滿足克萊因-戈登方程□2Φ(x,t)=0.本文利用克萊因-戈登方程推導兩質子之間的庫侖勢.
對於一個連續電荷分布,我們可以將每一個無窮小的空間元素視為一個電量為的點電荷,做無限求和。這程式等價於連續電荷分布的區域積分。
線電荷分布(例如,一根帶電的直線)的電量為
;
其中,是位於的線電荷密度(每單位長度所帶的電量),是一個無窮小線元素。
表面電荷分布(例如,兩平行金屬板電容器的一片帶電的金屬板)的電量為
;
其中,是位於的面電荷密度(每單位面積所帶的電量),是一個無窮小面積元素。
體積電荷分布(例如,一個帶電的圓球)的電量為
;
其中,是位於的體電荷密度(每單位體積所帶的電量),是一個無窮小體積元素。
作用於一個電量為的檢驗電荷的靜電力,可以表達為
。
其中,是檢驗電荷的位置,是位於的無窮小電荷元素。
就是電場造成的電勢能,庫侖力就是帶電粒子受的力,勢能就是力乘以質量再乘以受力的距離,你可以類比重力勢能,E=mgh
庫侖排斥勢能公式=K·Qq/r.庫侖力為F=K·Qq/r².那個質量呢
額 寫錯了 電勢能自然是電荷,不是質量
公式上庫侖排斥勢能是庫侖力乘距離
萬有引力計算公式:F=GMm/(R^2) 不是差不多,類比下就行了
勢能是力乘位移,比如說重力勢能是mgh。重力為mg,故此處為庫侖力乘r.