基本信息
Narayanan等人與1996年首次將量子理論與進化算法想結合，提出了量子遺傳算法（QIGA）的概念；2000年，Han等人提出了一種遺傳量子算法（GQA）,然後又擴展為量子進化算法（QEA），實現了組合最佳化問題的求解。
QEA採用量子比特編碼，一個量子比特表示為|ψ>=α|0+β|1>,α和β為複數，在第t代的染色體種群為
Q(t)={(q1)^t ， (q2)^t ，…… ，(qn)^t}
其中n為種群大小；t為進化代數，(qj)^t為染色體，即
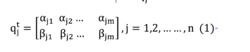公式1式中：m表示染色體長度，滿足|αji|^2 + |βji|^2 = 1。算法流程描述如下：
Begin
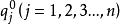量子進化算法
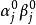量子進化算法1） t = 0,初始化種群Q(0),所有 中的 都被初始化為(1/√2, 1/√2)。
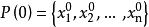量子進化算法
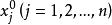量子進化算法
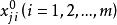量子進化算法
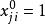量子進化算法2） 對初始種群中的各個體實施測量，得到一組狀態 . 是長度為m的串，每一位 為0或1，是根據量子比特的機率|αji|^2或|βji|^2測量得到的。測量過稱為：隨機產生一個數r,。若r屬於[0,1],則測量結果 ；否則，取0。
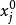量子進化算法3） 對各狀態f( )進行適應度評價。
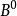量子進化算法 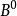量子進化算法4） 記錄下最佳個體狀態 及其適應度值f( )。
5）While非結束狀態do
Begin
1.t = t +1 ;
2.對種群Q(t-1)實施測量，得到一組狀態P(t);
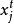量子進化算法3.對各狀態f( )適應度評價；
4.利用量子門U(t)更新Q(t);
5.保存B(t-1)和P(t)中的最佳解到B(t);
6.記錄下B(t) 中最佳個體狀態b
End
End
主要研究成果
QEA算法具有種群分散性好、全局搜尋能力強、收斂速度快且易於與其他算法融合等優點。近幾年，國內外許多重要文獻對QEA算法進行了更近一步的研究，主要體現在以下幾方面。
算法機理及性能研究
這類研究大多從分析QEA算法的運行機理入手，類比分析QEA與其他經典進化算法的區別和相似性。具有代表性的有Ming等人從機率角度分析QEA，從量子的“波粒二象性”分析量子在進化過程中的特點，將傳統遺傳算法（GA）和QEA藉助“波粒二象性”特徵進行了類比，如表1所示:
QEA,GA波粒二象性類比從表1可以看出：QEA的進化與GA的進化在本質上具有相似性，QEA的種群是由量子組成的機率系統，其個體適應度評價為量子的能量，進化過程是量子的熵和能量的一種競爭，最終求得最優解時量子熵降低，種群趨於聚集，進化過程是種群從一種不平衡狀態到平衡狀態的轉變。QEA進化的本質是種群的量子處於不確定狀態到最終確定狀態的過程，量子檢測到為0或者1的機率趨於確定，其熵值也趨於最小。另外，文獻[3] 利用量子的糾纏態理論解釋說明了遺傳算法的本質，認為遺傳算法計算在本質上是一種量子並行計算。Michael和Zhou等人都從分散式估計算法（EDA）的角度分析了量子進化算法，認為兩種算法共同特徵是利用機率模型進行演算，並從機率模型、抽樣選擇、學習替換和種群結構等方面進行了類比，得出了QEA的實質是一種EDA的結論。
通過圖1的比較可以看出：EDA通過個體分布建立機率模型，並利用該機率模型進行樣本採樣以產生新種群；而在QEA中，則通過對量子比特的機率幅測量、坍縮的方法產生新種群，坍縮的方法與EDA樣本採樣相對應，它能使種群向更高適應度方向進化。從實驗分析得出，QEA相對EDA更具有優勢，主要體現在以下兩方面：一是量子編碼樣本具有多樣性；二是其機率模型具有自適應性調節能力。另外，KaiFan等人對QEA算法的特性進行了分析，對比了QEA與經典遺傳算法、粒子群算法在解決靜態、動態函式最佳化問題的性能差別，並分別測試了二進制、十進制編碼情況下這幾種算法對低維、高維函式的最佳化效果。結果表明：在靜態環境下，QEA求解結果和運行時間都優於其他幾種算法；在動態環境，QEA穩定性更好，且運行時間更少，改進的QEA算法更適合動態環境下高維實空間問題。
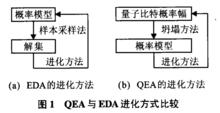QEA與EDA進化方式比較種群改進
量子比特編碼能用較小的種群規模表示問題的多個解，所以種群的規模、結構等對算法性能影響較大。此類研究主要可歸納為如下幾方面：
量子進化算法1)種群結構的改進。Najaran等人將QEA的種群結構進行了分類。按圖2所示可分為：環型、格線型、二叉樹型、簇型、方格型、 型、階梯型和交叉階梯型等。文獻[2] 利用測試函式尋優對比分析了不同種群結構算法的性能，結果表明格線型為QEA性能最好的種群結構。Alba等人講格線型的種群結構細分為正方形、長方形、長條形等，設計了根據個體適應度值和群體的熵來動態調節群體結構的QEA，這種算法能很好地兼顧勘探和開採能力。Ali Nodehi等人提出了基於格線結構的QEA，在這種結構中每個節點表示一個個體，這種結構能保持種群的多樣性，可有效避免早熟和陷入局部極值。另外，Guo等人利用複雜網路理論類比量子進化中的各個個體間關係，複雜網路中小世界原理為量子進化個體間關係提供了一種借鑑，為達到這種種群弱連結，算法將種群分解為局部小群，各小群進行局部進化，這種種群結構能有效避免算法早熟。
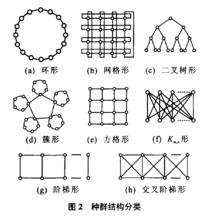種群結構分類2) 種群大小的改進。Ali Nodehi等人利用函式動態改變QEA種群大小。當種群增加時，隨機新加入的種群改善了種群的多樣性；當種群減少時，去掉種群中比較差的個體，可以縮小搜尋範圍，加快算法的收斂。Tayarani等人利用環形作為種群結構，以保證每個個體只與2個鄰居相鄰，並在進化過程中使用正旋函式改變種群大小，以保持種群多樣性。Imabeppu等人在粗粒度並行量子遺傳算法的基礎上，針對種群間個體遷移的方式，提出了一種成對交換的算法，該算法與局部、全局優秀個體遷移不同，它在所有種群個體中只選擇n/2對個體進行交換。對0-1問題的求解證明了所提出的算法具有局部搜尋和全局搜尋的優勢。
編碼擴展
表2,圖3，圖4
量子進化算法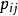
量子進化算法
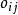量子進化算法
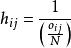量子進化算法
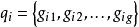量子進化算法QEA算法設計之初為量子比特編碼，在進化中測量產生二進制串，所以算法對多參數和高維問題的求解受到了限制。QEA編碼的擴展成為研究的熱點，一些具有代表性的改進可歸納如下：1) 機率實數編碼。Cruz等人定義了一種實數編碼方式的QEA，該思想是將個體中每個分量用 表示取值空間，它表示為一矩形區域，其中 表示變數取值的坐標中心，為矩形取值空間的寬度，矩形的高度為 ,N為變數個數，個體表示為 。該編碼利用高度表示機率，例如表2表示的是兩個體q1，q2的初始值。圖3表示了表2中兩個體q1，q2和機率實數編碼。圖3中，個體q1由中心為-5，寬度為20的g11矩形框及中心為0，寬度為20的g12矩形框組成。圖4表示兩個體q1，q2和進行交叉的結果。從圖4可以看出，當2個個體進行交叉時，是將q1，q2分別代表的矩形區域進行疊加來產生新的個體，疊加後的矩形框高度表示在該區域取值的機率。用這種方式編碼的量子進化算法，對高維函式最佳化測試結果顯示具有更好的收斂速度和尋優精度。覃朝勇等人在此基礎上引入了勢能的概念，並用於高維函式最佳化，也取得了較好的性能。
2）三倍體編碼。Li等人提出了一種量子位Bloch球面坐標編碼。圖5表示Bloch球中的一個點對應一個量子比特，因此量子比特|ψ>可描述為
|ψ>=[cosΦsinθ sinΦsinθcosθ]^T
按照這種方式，將量子位的3個Bloch球面坐標作為基因位，則可將量子比特編碼轉換為Bloch球面編碼，表示如下：
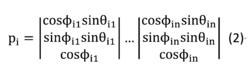將量子比特編碼轉換為Bloch球面編碼
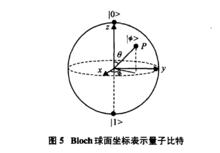圖5 Bloch球面坐標表示量子比特這種編碼能夠避免因對量子位測量產生二進制串所帶來的隨機性，可用於連續最佳化問題，能夠擴展全局最優解的數量，提高獲得全局最優解的機率。另外，高輝等人提出了一種三倍體實數編碼，即該編碼由自變數的一個分量與量子比特組成，算法設計了互補雙變異運算元來進化個體，這種運算元融合了量子旋轉門和量子比特歸一化條件，實現了局部搜尋與全局搜尋的平衡。
(3) 混合二倍體編碼。Zhao等人採用改進的二倍體編碼形式，即
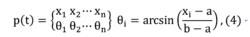改進的二倍體編碼形式
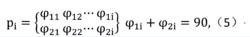混合二倍體編碼其中x屬於[a,b]為定義域區間，是實數。該文利用這種編碼提出了一種基於QEA的模糊神經網路模型。另外，申抒含等人提出一種多進制機率角複合位編碼QEA，將量子位的機率幅表示法轉化為複合位的機率角表示法，採用隨機觀測方法得到觀測個體，採用機率角增減的方式對個體進行更新。其編碼形式為其中0<φ1iφ2i<90。該算法適用於採用任意進制編碼問題。實驗表明，算法在適用範圍、搜尋能力和運算速度上均具有較為明顯的優勢。
運算元創新
基本QEA與一般進化計算不同，沒有選擇、交叉、變異等運算元，所以修改並提出新運算元融入QEA中便成為研究方向，具有代表性的有：
1） 粒子群運算元。Wang和周殊等人採用粒子群最佳化運算元調節量子旋轉門，並根據QEA自身機率特性，引入了最優解方差函式來評價該算法的穩定性。
2） 免疫算法。Hongjian 等人將免疫的概念引入QEA，免疫運算元在保留原算法優良特性的前提下，力圖有選擇、有目的地利用待求問題中的一些特徵信息或先驗知識，抑制或避免求解過程中的一些重複或無效的工作，以提高算法的整體性能。Haoteng等人提出了基於混沌理論的免疫QEA，該算法套用混沌免疫理論並依據小生境機制將初始個體劃分為實數編碼染色體的子群，各子群套用免疫運算元的局域搜尋能力找出最佳化解。
3） 克隆運算元。李陽陽等人提出一種基於量子編碼的免疫克隆算法來求解SAT問題，算法中採用量子位的編碼方式表達種群中的抗體，採用量子旋轉門和動態調整旋轉角策略對抗體進行演化，加速原有克隆運算元的收斂，利用克隆運算元的局部尋優能力強的特點，在各個子群體間採用量子交叉操作來增強信息交流，以提高種群的多樣性，防止早熟。
4） 模擬退火、模糊運算元，王毅等人借鑑模擬退火方法，根據進化代數及個體的適應度值修正傳統QEA旋轉門函式的旋轉角度值，焦嵩鳴等人利用模糊推理的方法，自適應地提高了算法的計算精度和收斂速度。
5） 文化運算元，Cruz等人在QEA中引入了文化運算元，該思想借鑑了文化算法中規範知識的概念，用以描述當代種群的有效搜尋空間範圍，規範知識可以規避不在該範圍內個人，引導個體進入有效區域搜尋，算法收斂速度和精度都得到了提高。
6） 其他運算元。AraujoM等人利用多目標最佳化對量子進化中的旋轉角參數進行計算，算法分2個層次，上層為求解多個測試函式的旋轉角和旋轉方向參數，將得到的參數用於底層的量子進化最佳化過程。Xing等人利用兩點交叉運算元對量子旋轉門調整進行改進，其核心思想是確保在任何狀態下以較大的機率使當前解收斂到一個具有更高適應度的染色體。
